Pythagoras

গত কাল ধর্ম নিয়ে একটা পোষ্টে পিথাগোরিয়জম ব্রাদার হুডের কথা বলেছিলাম, আজকে আর এক পিথাগোরাসের উল্লেখ্য করব, অবশ্য এই পিথাগোরাস সবার চেনা কিন্তু অজানা কিছু কাজ (হয়ত কেউ কেউ জানেন তবে অনেকেই জানেন না)। গনিতের বিস্ময়কর কার্যকারিতা নিয়ে যিনি প্রথম উপলদ্ধি করেছিলেন, তিনি হলেন পিথাগোরাস। “সংখ্যাই শেষ কথা” এই ছিল তার বানী।

প্রকৃতির সাথে সংখ্যার যে সম্পর্ক তা তিনি দেখিয়েছিলেন চমৎকার এক পরীক্ষার মাধ্যমে। পানি পূর্ন একটি কলসির গায়ে তিনি হাতুড়ী দিয়ে আঘাত করে শব্দ তৈরী করেন। এর পর ওই কলসি অর্ধেক পুর্ন করে আবার আঘাত করে শব্দ শোনেন, দেখা যায় শব্দ দুটোর শ্রুতি মধুর, এরপর একে একে তিন ভাগের এক ভাগ, চার ভাগের এক ভাগ পূর্ন করে শব্দ করে দেখেন তাও বেশ শ্রুতি মধুর।

যদি গনিতে লিখি তবে ১/১, ১/২, ১/৩, ১/৪ পূর্ন সংখ্যার অনুপাত করলে লেখা যায় ১,২,৩,৪

কিন্তু পিথাগোরাস দেখান কলসিতে অন্য মাপে পাচ ভাগের তিন ভাগ বা আট ভাগের পাচ ভাগ পানি পূর্ন করে শব্দ সৃষ্টি করলে তা বেসুরো শোনায়।

যদি গনিতে লিখি তবে ৩/৫, ৫/৮ যা পূর্ন সংখ্যায় প্রকাশ করা যায় না। তার মানে কি দাড়াচ্ছে? সুন্দরের প্রতীক যে সঙ্গীত তাও কিন্তু গনিত নির্ভর।

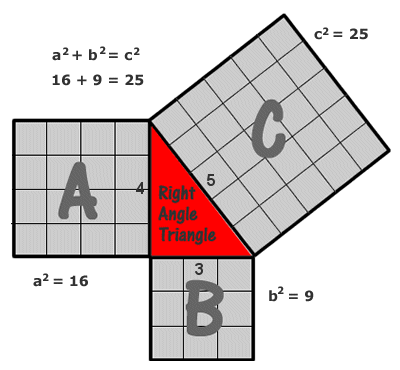
বাস্তবের সাথে গনিতের আর একটি নিদর্শন যা জ্যামিতির মাধ্যমে প্রমান করে বিখ্যাত হয়ে আছেন এই পিথাগোরাস। তার বিখ্যাত উপপাদ্য যা এক কালে খুব জ্বালাতন করছে আমি সহ এই ব্লগের প্রায় সবাইকেই। সবাই জানেন সেই উপপাদ্যটি “কোন সমকোনী ত্রিভুজে অতিভুজের ওপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল অন্য দুটি বাহুর ওপর আঁকা বর্গক্ষেত্রের ক্ষেত্রফলের সমান।” এটা তো গেল জ্যামিতির কথা কিন্তু এর সাথেও সংখ্যার সম্পর্ক আছে আমরা কয়জন তা জানি?

যে কোন সমকোনী ত্রিভুজের বাহুগুলো একটা নির্দিষ্ট নিয়ম মানতে বাধ্য। ত্রিভুজটির ছোট দুই বাহুর দৈর্ঘ্য যদি ৩ মিটার এবং ৪ মিটার হয় (ফুট বা অন্য কোন একক ও হতে পারে) তবে সব চেয়ে বড় বাহু মানে অতিভুজের দৈর্ঘ্য ৫ মিটার হতেই হবে। কেন? সংখ্যাগুলো পর পর বলে মানে ৩,৪,৫ বলে? না, তা না। বাহুগুলো ৫ মিটার, ১২ মিটার, ১৩ মিটার ও হতে পারে। পিথাগোরাস দেখান যে ৩,৪,৫ বা ৫,১২,১৩ র মাঝে একটা সম্পর্ক বয়েছে, কী রকম সে সম্পর্ক?

৩² + ৪² = ৩ X ৩ + ৪ X ৪ = ৯ + ১৬ = ২৫ = ৫²

অর্থ্যাৎ ৩² + ৪² = ৫²

ঠিক তেমনই ৫² + ১২² = ৫ X ৫ + ১২ X ১২ = ২৫ + ১৪৪ = ১৬৯ = ১৩²

অর্থ্যাৎ ৫² + ১২² = ১৩²

আপনি যদি সমকোনী ত্রিভুজের বাহুগুলোর ওপর বর্গ একে দেখেন তবে দেখবেন হিসাব মিলে যাচ্ছে। সমকোনী ত্রিভুজের তিনটা বাহু এক রহস্যময় কারনে একে অপরের সাথে সম্পর্কিত।

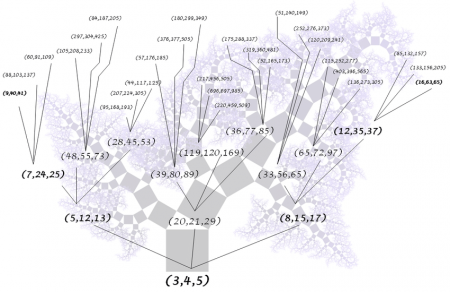
Tree of primitive Pythagorean triples

পিথাগোরাসের শিষ্যরা গুরুর উপপাদ্য নিয়ে চর্চা করার সময় একটা জিনিস লক্ষ্য করলেন এই শেকলে বাধা তিন সংখ্যার শেষ নেই ৩,৪,৫ বা ৫,১২, ১৩ র উদাহরন তো আগেই দিয়েছি এ রকম আরো অসংখ্য তিন সংখ্যা আছে ৬-৮-১০, ৯-১২-১৫, ১০-২৪-২৬, ১৫-৩৬-৩৯, ২০-৪৮-৫২ ......... একই রকম শর্ত মেনে চলে, আরো একটা উদাহরন দেই

১৫² + ৩৬² = ১৫ X ১৫ + ৩৬ X ৩৬ = ২২৫ + ১২৯৬ = ১৫২১ = ৩৯²

The Library of Alexandria Is Long-Gone

এই যে বিশেষ সম্পর্কে আবদ্ধ তিনটি করে সংখ্যা যাদের দুইটির বর্গের সমষ্টি তৃতীয়টির বর্গের সমান তাদের একত্রে বলা হয় “পিথাগোরিয়ান ট্রিপল”। গ্রীক গনিতবিদ দিওফান্তাস প্রাচীন পাটি গনিতের এই সব মনিমুক্তা সব এক করে খ্রিষ্টপূর্ব দ্বিতীয় শতকে একটি ১৩ খন্ডের একটা বিশাল বই লেখেন যার নাম “এ্যারেথমেটিকা”। ওই এ্যারেথমেটিকাতে এই পিথাগোরিয়ান ট্রিপল নিয়ে বিশাল এক আলোচনা আছে। আলেকজান্দ্রিয়ার বিখ্যাত লাইব্রেরীতে সেই বইটি রক্ষিত ছিল।

মিশরের রানী ক্লিওপেট্রার সাথে জুলিয়াস সিজারের যুদ্ধ লাগলে, সিজার ক্লিওপেট্রার নৌবহরে আগুন লাগিয়ে দিলে নৌবহরের সাথে সাথে বন্দর সংলগ্ন লাইব্রেবীতে আগুন লেগে মানব ইতিহাসের অনেক অমুল্য সম্পদ নষ্ট হয়ে যায়, পরে ক্লিওপেট্রার প্রেমিক মার্ক এ্যান্টনি ওই লাইব্রেরী আবার পূর্নগঠনের চেষ্টা করেন কিন্তু ততদিনে “এ্যারেথমেটিকার” সাত খন্ড নষ্ট হয়ে যায়। টিকে থাকে ছয় খন্ড। ফরাসি পন্ডিত ক্লদ গ্যাসপা বাশে এর ল্যাটিন অনুবাদ করেন। এই বই খানি খুব প্রিয় ছিল ফরাসী গনিতবিদ পিয়েরে ফার্মার।

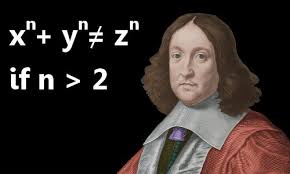
Pierre de Fermat

সারাদিন কাজ কাম শেষ করে শখের গনিতবিদ পিয়েরে ফার্মা ডুবে যেতেন পিথাগোরাসের এই “এ্যারেথমেটিকা” নিয়ে। মৌলিক সংখ্যা নিয়ে তিনি একটি ধাঁধা জানালেন এক গনিত পন্ডিত কে ধাধাটি এরকমঃ

আমরা জানি, ২,৩,৫,৭,১১...... এগুলো মৌলিক সংখ্যা। এবার –

৪² - ৪ = ১৬ – ৪ = ১২ এই ১২ কে ২ দ্ধারা ভাগ দিলে কোন ভাগ শেষ থাকে না (পাঠক একটু খেয়াল রাখেন ৪ এর ঘাত ২)

তেমনি ৬³ - ৬ = ৬ X ৬ X ৬ -৬ = ২১৬-৬ = ২১০ ফলাফল ৩ দ্ধারা বিভাজ্য (পাঠক একটু খেয়াল রাখেন ৬ এর ঘাত ৩)

৭^৫ – ৭ = ৭ X৭ X৭ X৭ X৭ – ৭ = ১৬৮০৭ – ৭ =১৬৮০০ ফলাফল ৫ দ্ধারা বিভাজ্য (পাঠক একটু খেয়াল রাখেন ৭ এর ঘাত ৫)

কিন্তু ঘাত (এখানে ঘাত বলতে ছোট করে সংখ্যাগুলো লেখা হয়েছে তাই বুজানো হয়েছে) ২,৩,৫,৭ ইত্যাদি মৌলিক সংখ্যা না হলে ব্যাপারটা আর এ রকম ঘটে না।

যেমনঃ ৪^৬ – ৪ = ৪ X ৪ X ৪ X ৪ X ৪ X ৪ – ৪ = ৬৬৫৬ – ৪ = ৬৬৫২ ( সংখ্যাটি ৬ দ্ধারা বিভাজ্য না)।

অর্থ্যাৎ দেখা যাচ্ছে যে কোন সংখ্যার মৌলিক ঘাত থাকলে সংখ্যাটির বিয়োগফল ওই মৌলিক ঘাত দিয়ে বিভাজ্য। কিন্তু ঘাত মৌলিক না হলে এই নিয়ম আর খাটবে না, খাটবে না কেন তা কি যুক্তি দিয়ে প্রমান করা যায়? ফার্মা চ্যালেঞ্জ ছুড়ে দিলেন তার গনিতবিদ বন্ধুদের দিকে।

“পিথাগোরিয়ান ট্রিপল” নিয়ে পড়াশুনা করতে করতে ফার্মার মনে এক অদ্ভুত চিন্তা আসল
৩² + ৪² =৫²
৬² + ৮² = ১০²
.........
৫² + ১২² = ১৩²
১০² + ২৪² = ২৬²
........
২০² + ২১² = ২৯²
৪০² + ৪২² = ৫৮²

আচ্ছা ঘাত এর জায়গায় ২ না হয়ে যদি ৩ হয় তা হলে কি মিলবে? দেখা যাকঃ

৩³ + ৪³ = ৫³
২৭ + ৬৪ = ১২৫
৯১ = ১২৫ না মিলছে না।

ঘাত ৪, ৫, ৬, ৭ হলেও মিলছে না। ফার্মা দেখলেন ঘাত ২ এর বেশী হলেই এমন তিনটি সংখ্যা আর খুজে পাওয়া যাচ্ছে না যেখানে দুটো সংখ্যার ঘাতের যোগফল তৃতীয় সংখ্যার একই ঘাতের সমান হয়। সংখ্যার শেষ নেই, ঘাতের ও শেষ নেই। ফার্মার মনে হল “পিথাগোরিয়ান ট্রিপলের” ঘাত যদি ২ এর বড় হয় তবে দুটো সংখ্যার ঘাতের সমষ্টি তৃতীয় সংখ্যার ঘাতের সমান হবে না। এই পর্যন্ত যদি ঘটনা থাকত তবে তা ইতিহাস হত না।

ফার্মার একটি অদ্ভুত স্বভাব ছিল গনিতের কাজ করতে করতে সেই বইর মার্জিনে কোন সমাধান বা সমস্যা হলে তা লিখে রাখত, দিওফান্তেসের “এ্যারিথমেটিকা”য় ও এর ব্যাতিক্রম হলনা।

The 1670 edition of Diophantus's Arithmetica includes Fermat's commentary, referred to as his "Last Theorem" (Observatio Domini Petri de Fermat), posthumously published by his son.

কিন্তু ইতিহাসের শুরু এখান থেকেই, ফার্মা মারা যান ১৬৬৫ সালের ১২ ই জানুয়ারী তখন তার ছেলে ফার্মার সব গবেষনা এক করে ১৬৭০ সালে একটি বই প্রকাশ করেন নাম “দিওফান্তেস এ্যারিথমেটিকা কনটেনিং অভজারভেশান বাই পীয়ের দ্যা ফার্মা”। সেখানে “এ্যারিথমেটিকার” মার্জিনে ফার্মা ছোট্ট একটা মন্তব্য লিখে যান “এই প্রতিপাদ্যটির চমৎকার একটি সমাধান আমার হাতে আছে, কিন্তু এই মার্জিনের পরিসর এত ছোট যে তা এখানে ধরবে না।” শখের গনিতবিদ ফার্মা তো লিখেই খালাস কিন্তু মাথা খারাপ করে দিল গনিতবিদদের। বাঘা বাঘা গনিতবিদরা গত সাড়ে তিনশত বছর এনিয়ে মাথা ঘামিয়ে কুল পেল না। কিংবদন্তী হয়ে গেল ফার্মাস লাষ্ট থিওরেম সংক্ষেপে ( এল এফ টি)।

ফার্মা তাঁর জীবনে খুব রহস্যময় চলাফেরা করতেন। কেউ কেউ ভাবলেন এই সমস্যাটা নিয়েও হয়তো তিনি রহস্য করে এটা লিখেছিলেন। হতে পারে সমস্ত গণিত দুনিয়ার সাথে এটা একটা রসিকতা। কেউ কেউ মনে করলেন সত্যিই হয়তো তিনি সমাধান পেয়েছিলেন। ফার্মার এই নোটের কারণে সমস্যাটি আরো রহস্যময় ও জনপ্রিয় হয়। তখন থেকে অনেকে লেগে পড়েন কী ছিল সেই সমাধান? ১৬৩৭ সাল থেকে শুরু করে দীর্ঘদিন পর্যন্ত কেউ এই সমস্যার সমাধান করতে পারেননি।

ইনাম ঘোষিত হল কেউ যদি এল এফ টির সমাধান দিতে পারে তবে সে পাবে এক মিলিয়ন ডলার। লিওনার্দো অয়েলার ১৭৪২ খ্রিষ্টাব্দে তার এক গনিতবিদ বন্ধুকে চিঠি লিখে অনুরোধ করলেন ফার্মার বাসায় তল্লাশী চালাতে এল এফ টির প্রমান সম্বলিত কোন ক্লু টুলু যদি কোথাও পাওয়া যায়। এই এল এফ টি নিয়ে অনেক অনেক মীথ আছে আজকে শুধু ফার্মার লাষ্ট থিওরেম টা আপনাদের জন্য উপস্থাপন করলাম, জানি না কতটা বোধ গম্য হয়েছে, তবে গনিতে এমন আরো কিছু ধাঁধা আছে ভালো লাগলে সামনে নিয়ে আসব।

Sir Andrew John Wiles

নোটঃ শত শত বছর ধরে এটি নানান গণিতবিদদের আগ্রহী করেছে, ঘুম নষ্ট করেছে, ব্যর্থ করেছে। অনেকগুলো বছর পর ১৯৯৩ সালে এন্ড্রু উইলস এই সমস্যাটির একটি সমাধান উপস্থাপন করতে সমর্থ হন।

এন্ড্রু উইলস যখন খুব ছোট তখন থেকেই ফার্মার এই উপপাদ্য নিয়ে আগ্রহী হয়ে ওঠেছিলেন। শুধু আগ্রহীই না, বলা যায় অন্ধভাবে আগ্রহী হয়ে ওঠেন। এই সমস্যাটি সমাধানে প্রচুর সাধনা করেন। তার ভাষায় “এই সমস্যাটি আমাকে এক ধরনের মোহে আবিষ্ট করে ফেলেছিল।”

১৯৯৩ সালের ২৩ শে জুন তিনি তাঁর আবিষ্কারের কথা বিশ্ববাসীকে জানালেন। বিশ্বের সেরা সব গণিতজ্ঞরা এন্ড্রু ইউলসের প্রমাণ দেখলেন, চুলচেরা বিশ্লেষণ করতে লাগলেন। পৃথিবীর সবচেয়ে জটিল সমস্যাটির সমাধান। ২০০ পৃষ্ঠায় তিনি তাঁর সমাধান তৈরি করে পাঠালেন ‘ইনভেনশন ম্যাথমেটিক’ জার্নালে ছাপানোর জন্য। ছাপানোর আগে যেকোনো বৈজ্ঞানিক নিবন্ধই দুই বা তিনজন দক্ষ বিশেষজ্ঞদের দেওয়া হয় রিভিউয়ের জন্য। কিন্তু পৃথিবীর সবচেয়ে জটিল এই সমাধান রিভিউর জন্য নির্বাচন করা হলো ছয়জন গণিতবিদ।

তাও পুরোটি কারো কাছে দেওয়া হলো না। এক একজনকে দেওয়া হলো একটিমাত্র অধ্যায়। নিক কাটজ (Nic Katz) এর হাতে পৌছলো এর তৃতীয় অধ্যায়। কিন্তু এই অধ্যায়টি সম্পূর্ণ ত্রুটিমুক্ত রইলো না। মারাত্মক ত্রুটি ধরা পড়লো। এ যে স্বপ্নপুরণের দ্বারপ্রান্তে এসে স্বপ্নভঙ্গের মতো ঘটনা। হতাশ হওয়ার মতোই ঘটনা। কিন্তু উইলস হতাশ হলেন না। স্বপ্নপূরণের সঙ্গী তাঁর প্রিয়তমা স্ত্রী নাডা (Nada) তাঁকে আশার বাণী শোনালেন, উৎসাহ যোগালেন। ১৯৯৩ সালের সেপ্টেম্বর মাসে উইলস-এর স্ত্রী নাডা তাঁকে জানালেন আসছে জন্মদিনে তাঁর একটাই চাওয়া, তাহলো ফার্মার শেষ উপপাদ্যের ত্রুটিমুক্ত সমাধান। এটাই হবে তাঁর জন্মদিনের সবচেয়ে মূল্যবান উপহার। প্রিয়তমা স্ত্রীর জন্মদিন ৬ই অক্টোবর। মাত্র দুই সপ্তাহ বাকি। উইলস এবারও ব্যর্থ হলেন। প্রিয়তমা স্ত্রীর জন্মদিনের উপহার দেওয়া হলোনা সেবার।

ঠিক এক বছর পরে, ১৯৯৪ সালের অক্টোবর মাসে এন্ড্রু জন উইলস সফল হলেন। এবারে তাঁর প্রমাণটি সম্পূর্ণরূপে ত্রুটিমুক্ত হলো। স্ত্রীর চাওয়া জন্মদিনের সবচেয়ে মূল্যবান উপহারটি পাওয়া গেল এক বছর পরে। আর বিশ্ববাসী পেল সাড়ে তিনশ বছরের পুরোনো, পৃথিবীর সবচেয়ে জটিলতম সমস্যাটির সমাধান।

দেখতে পারেন অংক সম্পর্কিত অংকের নোবেল

সুত্র এবং ছবিঃ অন্তর্জাল, এবং ভারতীয় বিজ্ঞান লেখক পথিক গুহ র একটা নিবন্ধ।।

ক্ষমাপ্রার্থনাঃ ঘাত লিখতে গিয়ে ইংরেজী বাংলা মিশে গেছে, আবার কিছু জায়গায় "^" চিহ্ন দিয়ে প্রকাশ করতে হয়েছে কারন সামুতে বাংলায় ঘাত লেখা সম্ভব না কোন এক অজ্ঞাত কারনে যেমনঃ চার স্কয়ার (৪²) লিখতে হয়েছে এখানে চারের ওপর বাংলায় স্কয়ার দিলে সেটা স্কয়ার থাকছে না ৪২ হয়ে যাচ্ছে। যার কারনে বাংলা ইংরেজী এবং "^" মিশিয়ে ঘাত প্রকাশ করতে হয়েছে। এটা আমার একান্ত অনিচ্ছাকৃত। সবাইকে ধন্যবাদ