কোটি কোটি মাইল জুড়ে বিস্তৃত ছায়াপথ, ধেয়ে আসা হারিকেন আর পা কেটে দেয়া পঁচা শামুক, অথবা আমাদের কর্ণকুন্ডলী- এদের মধ্যে আশ্চর্য এক মিল আছে। মিলটা আকারের- এদের প্রত্যেকের আকার একই রকম কুন্ডলাকৃতির।

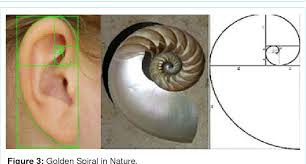
আবার এই কুণ্ডলাকৃতি তৈরি হয়েছে এক বিশেষ গাণিতিক নিয়ম মেনে।  কুন্ডলীর শুরু এক বর্গক্ষেত্রের বিপরীত কোণের মধ্যবর্তী বৃত্তচাপ দিয়ে, এরপর তার সাথে আরও নানা মাপের বর্গক্ষেত্র যোগ হয়, আর তাদের বিপরীত কোন এর মধ্যকার বৃত্তচাপ গুলো যোগ হয়ে, একের পর এক মিলে কুণ্ডলী তৈরি করে- ঠিক এই ছবির মতন।

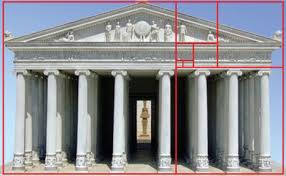
এই বর্গক্ষেত্রগুলোর বাহুর মাপ কিন্তু এলোমেলো কিছু নয়- এদের প্রত্যেকটার সাথে প্রত্যেকের অনুপাত একই। এই যে অনুপাত, এর নাম সোনালী অনুপাত বা স্বর্গীয় অনুপাত-  প্রকৃতিতে নানাভাবে এর দেখা মেলে। গ্রীক গণিতজ্ঞ ইউক্লিড এবং পিথাগোরাস প্রায় আড়াই হাজার বছর আগে প্রথম সোনালী অনুপাত লক্ষ্য করেন, সুষম পঞ্চভুজ আর পাঁচ কোনা বিশিষ্ট তারার আকার পর্যবেক্ষণের মধ্যে দিয়ে। সুষম পঞ্চভুজের কর্ণ ও বাহুর অনুপাত স্বর্গীয় অনুপাতের সমান, আবার পাঁচ কোনা বিশিষ্ট তারার বাহুগুলোও স্বর্গীয় অনুপাতে বিভক্ত হয়। এই গণিতজ্ঞরা প্রকৃতির নানা অনুষঙ্গে এই অনুপাত লক্ষ্য করেছিলেন। তারা এটাও দেখেছিলেন, এই অনুপাত ব্যবহার করে তৈরি আয়তক্ষেত্র (যার বাহুদ্বয়ের অনুপাত ১.৬১৮: ১) সবচাইতে নিখুঁত হয়। এই আয়তকে বলা হয় সোনালী আয়ত।  প্রাচীনকাল থেকেই ভাস্কর ও স্থপতিরা তাদের সৃষ্টিকর্মে এই অনুপাত ব্যবহার করেছেন, তারা কি গণিতজ্ঞদের এই পর্যবেক্ষণের কথা জানতেন, নাকি না জেনেই, কেবল দৃষ্টিনন্দন হয় বলেই এই অনুপাত মানতেন- আজ আর তা জানা যায় না। গ্রীক দেবী এথেনার মন্দির পার্থেননের নির্মাণে সোনালী আয়তর প্রয়োগ দেখা যায়।(এর বিপরীত মতও আছে)

পিরামিডেও আছে সোনালী অনুপাত। পিরামিডের ভূমির দৈর্ঘ্যকে এক একক ধরলে দেখা গেছে এর ঢালুতলের দৈর্ঘ্য ১.৬১৮ একক এবং উচ্চতা ১.৬১৮ এর বর্গমূল এর সমান একক। মধ্যযুগের অনেক স্থাপত্যে, সোনালী অনুপাতের প্রয়োগ দেখা যায়। রেনেসাঁ যুগের শিল্পী লিওনার্দো দ‍্য ভিঞ্চি, মাইকেল এঞ্জেলো, বত্তিচেল্লি তাদের চিত্রকর্মে স্বর্গীয় অনুপাত ব্যবহার করেছেন। বিংশ শতাব্দীতে সালভাদর ডালি তাঁর চিত্রকর্মে এই অনুপাত ব্যবহার করেছেন। দ‍্য ভিঞ্চির 'দ‍্য লাস্ট সাপার' চিত্রের নানা অনুষঙ্গে সোনালী অনুপাত দেখা যায়।

সোনালী অনুপাত নিয়ে বইও লেখা হয়েছে। সোনালী অনুপাত সম্পর্কে ফরাসি গণিতজ্ঞ লুকা পাচোলীর লেখা 'De divina proportione' বইয়ের ছবি এঁকেছিলেন লিওনার্দো দ‍্য ভিঞ্চি। তারও আগে, প্রথম খিস্টাব্দে রোমান সাহিত্যিক- স্থপতি- প্রকৌশলী মার্কাস ভিট্রুভিয়াস লিখেছিলেন De Architectura. এই বইটিতে লেখক আলোচনা করেছিলেন মানবদেহ ও নিখুঁত স্থাপত্যে যে এক অনুপম অনুপাত রয়েছে তা নিয়ে। এই বই পড়ে লিওনার্দো দ‍্য ভিঞ্চি উদ্বুদ্ধ হন তার বিখ্যাত চিত্রকর্ম the vitruvian man তৈরি করতে।

স্থাপত্য ও চিত্রকর্ম ছাড়াও সোনালী অনুপাত এর প্রয়োগ দেখা যায় ভাস্কর্যে। গ্রীক ভাস্কর ফাইডাস,(Phidias, ৪৮০-৪৫০ খৃষ্ট- পূর্বাব্দ) এই অনুপাত ব্যবহার করে এথীনা, জিউস প্রভৃতি দেবদেবীর মূর্তি গড়েছিলেন। এই ফাইডাসকে স্মরণ করেই বিংশ শতাব্দীর প্রথমদিকে সোনালী অনুপাতের নামকরণ করা হয় 'ফাই', আর আর গ্রিক বর্ণমালার ২১ তম বর্ণ কে ফাই এর প্রতীক হিসেবে ধরা হয়। ফাই কে সংজ্ঞায়িত করা হয় এভাবে- যদি দুটো সংখ্যার যে অনুপাত, আর তাদের যোগফল ও বড় সংখ্যাটির অনুপাত একই সমান হয়, তবে এই অনুপাতকে সোনালী অনুপাত বলে। অর্থাৎ, দুটি সংখ্যা যদি হয় ক এবং খ, (উভয়ই অশুন‍্য সংখ্যা) তবে,

ফাই= ( ক+খ)/ক= ক/খ

ফাই এর মান নির্ণয় করা হয় এভাবে,

ফাই= (১+√৫)/২= ১.৬১৮০৩৩৯৮৮৭.....................

পাই এর মতই ফাই এর মান কখনোই পুরোপুরি নির্ণয় করা যায় না, এটি একটি অমূলদ সংখ্যা। তাই দশমিকের পরে তিন দশমিক স্থান পর্যন্ত এটির আসন্ন মান ধরা হয়, অর্থাৎ ফাই= ১.৬১৮ ধরা হয়।


 প্রায় আড়াই হাজার বছর আগে গ্রিক গণিতবিদেরা সোনালী অনুপাতের কথা  জানতেন- সেই সোনালী অনুপাত আবার নতুন ভাবে পাওয়া যায় ত্রয়োদশ শতাব্দীতে, গণিতজ্ঞ লিওনার্দো ফিবোনাচ্চির আবিষ্কৃত সংখ্যাক্রম থেকে। একবছরে একজোড়া খরগোশের প্রজনন প‍্যাটার্ন নির্ণয় করতে গিয়ে ফিবোনাচ্চি এই সংখ্যাক্রম তৈরি করেন, যা তার নাম অনুসারে ফিবোনাচ্চি ক্রম (Fibonacci sequence/ Fibonacci series) নামে পরিচিত হয়।  সিরিজটা এরকম-

০, ১, ১, ২, ৩, ৫, ৮, ১৩, ২১, ৩৪, ৫৫, ৮৯, ১৪৪, ২৩৩, ৩৭৭..............

এই সিরিজ এর বৈশিষ্ট্য হচ্ছে, এর যে কোন সংখ্যা তার পূর্ববর্তী দুই সংখ্যার যোগফল, যেমন ৩= ২+১, ৫= ২+৩,  ৮= ৩+৫, এরকমভাবে। সিরিজের সংখ্যা গুলো নিয়ে নানারকম নিরীক্ষা চলে। দেখা গেল যে, এই সিরিজের পরপর নেয়া যেকোনো দশ সংখ্যার যোগফল এগার দিয়ে বিভাজ্য। যেমন,

০+১+১+২+৩+৫+৮+১৩+২১+৩৪=৮৮;

৩+৫+৮+১৩+২১+৩৪+৫৫+৮৯+১৪৪+২৩৩=৬০৫;

আবার যেকোনো ফিবোনাচ্চি সংখ্যার বর্গ থেকে তার দুই ধাপ আগের সংখ্যার বর্গ বিয়োগ করলে পাওয়া যায় একটি ফিবোনাচ্চি সংখ্যা, যেমন;

৮^২- ৩^২= ৬৪- ৯= ৫৫;
১৩^২- ৫^২= ১৬৯- ২৫= ১৪৪;

আবার ফিবোনাচ্চি সিরিজের সংখ্যাগুলো বর্গ করলে পাওয়া যায় এই সিরিজ:

১^২, ১^২, ২^২, ৩^২, ৫^২, ৮^২, ১৩^২, ২১^২......

এই সিরিজের সংখ্যাগুলো যদি ক্রমান্বয়ে এভাবে যোগ করি তাহলে দেখি-

১^২+১^২+ ২^২ = ৬ = ২*৩

১^২+ ১^২+ ২^২+ ৩^২= ১৫= ৩*৫

১^২+১^২+২^২+৩^২+৫^২= ৪০= ৫*৮

১^২+১^২+২^২+৩^২+৫^২+৮^২= ১০৪= ৮*১৩

১^২+১^২+২^২+৩^২+৫^২+৮^২+১৩^২=২৭৩= ১৩*২১
..........................
...........….............
এখানে প্রতিটা  যোগফল দুটো সংখ্যার গুণফল, এই গুণফলগুলো আবার একটা প্যাটার্ন মেনে চলেছে, যে প্যাটার্নে সব সংখ্যাগুলোই ক্রমিক ফিবোনাচ্চি সংখ্যা!!!!

ফিবোনাচ্চি এই সংখ্যাগুলো পর্যবেক্ষণ করতে গিয়ে  সিরিজের একেকটি সংখ্যাকে  তার আগের সংখ্যা দিয়ে ভাগ করতে লাগলেন (প্রথম সংখ্যা শূন্য বাদে)। দেখা গেল ভাগফল ক্রমান্বয়ে একটা সংখ্যার  সমীপবর্তী হচ্ছে, এভাবে:

৩/২=১.৫....... ৫/৩=১.৬৬৭........৮/৫=১.৬......

১৩/৮=১.৬২.........২১/১৩=১.৬১৫......

৩৪/২১=১.৬১৯........৫৫/৩৪=১.৬১৭......

৮৯/৫৫=১.৬১৮.......১৪৪/৮৯=১.৬১৭৯......

২৩৩/১৪৪=১.৬১৮......৩৭৭/২৩৩=১.৬১৮......

অর্থাৎ ফিবোনাচ্চি সিরিজের পরপর দুটি সংখ্যার দ্বিতীয়টিকে প্রথমটি দিয়ে ভাগ করতে থাকলে একসময় ভাগফলের আসন্ন মান দাঁড়ায় ১.৬১৮ এর কাছাকাছি। এভাবে  লিওনার্দো ফিবোনাচ্চি তার সিরিজ থেকে ফাই এ পৌঁছান। অবশ্য পরে দেখা গেছে, সোনালী অনুপাত ফাই যে কেবল ফিবোনাচ্চি সিরিজ থেকেই পাওয়া যায় তা নয়, বরং যেকোনো random দুটি সংখ্যা নিয়ে, তাদের যোগফল দিয়ে তৃতীয় সংখ্যা ধরে এভাবে series তৈরি করে, পূর্ববর্তী সংখ্যা দিয়ে পরবর্তী সংখ্যাকে ভাগ করতে করতে একসময় ভাগফল ফাই এর কাছাকাছি হয়। তবে এক্ষেত্রে ফিবোনাচ্চি সিরিজের মতো এতো তাড়াতাড়ি ভাগফল ফাই হয়না। আজ জুলাই মাসের ২৯ তারিখ, ৭ আর ২৯ এই দুটো সংখ্যা নিয়ে একটা সিরিজ বানালে এমন হবে:

৭, ২৯, ৩৬, ৬৫, ১০১, ১৬৬, ২৬৭, ৪৩৩, ৭০০, ১১৩৩, ১৮৩৩...............

পরপর সংখ্যাগুলোর দ্বিতীয়টিকে প্রথমটি দিয়ে ভাগ করলে ভাগফল দাঁড়াবে এরকম:

৪.১৪২......, ১.২৪......, ১.৮০......, ১.৫৫........, ১.৬৪৩৫.........., ১.৬০৮৪....., ১.৬২১৭........, ১.৬১৬৬..........,
১.৬১৮৫......., ১.৬১৭৮......, এভাবে এই সিরিজ থেকেও একসময় ফাইয়ের কাছে পৌঁছানো যায়।

ফাই- এর বৈশিষ্ট্যগুলোও বিস্ময়কর, যেমন:

১+ ফাই = ২.৬১৮ = ( ফাই )^২

 ফাই -১ = ০.৬১৮ = ( ফাই )^-১

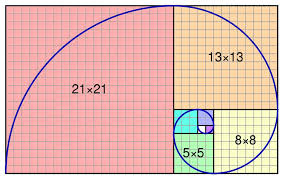
তাহলে, এখন ফিবোনাচ্চি সিরিজের দুটো পরপর সংখ্যা বাহু নিয়ে যদি হয় একটি আয়তক্ষেত্র, তবে সেই আয়ত হবে সোনালী আয়ত। (যেমন প্রথম ছবিতে, ৩৪*২১ বর্গ একক)। সেই আয়তকে  আবার ক্রমান্বয়ে বর্গক্ষেত্র ও ছোট আয়ততে ভাগ করা যায়, যতক্ষণ না ফিবোনাচ্চি সংখ্যা ১ ও ২ একক দৈর্ঘ্যের বাহু বিশিষ্ট আয়ত  পাওয়া যায়। ভাগ করার পর যে আয়তক্ষেত্র ও বর্গক্ষেত্র পাওয়া যাচ্ছে তা এমন:

    আয়তক্ষেত্র                    বর্গক্ষেত্র
     (বর্গ একক)                     (বর্গ একক)
      ২১*১৩                          ২১*২১
      ১৩*৮                            ১৩*১৩
         ৮*৫                               ৮*৮
         ৫*৩                                ৫*৫
         ৩*২                                ৩*৩
         ২*১                                 ২*২ 
সবশেষে দুটো ১*১ বর্গক্ষেত্র।

অর্থাৎ সোনালী আয়তর ভিতরে আঁকা আয়তগুলি ক্ষুদ্রাতিক্ষুদ্র মাপে ভাগ করলেও সোনালী আয়তই হয়ে থাকে, যেমন পার্থেননের মন্দিরের ছবিতে দেখা যাচ্ছে।

ফিরে যাই সোনালী অনুপাতে। আমাদের শরীরের নানা ভাবে সোনালী অনুপাত এবং ফিবোনাচ্চি সংখ্যা দেখা যায়, আমি তার থেকে কয়েকটা উল্লেখ করছি।

কনুই থেকে কব্জি পর্যন্ত দৈর্ঘ্য/ কব্জি থেকে আঙ্গুলের আগার দৈর্ঘ্য= ১.৬১৮।

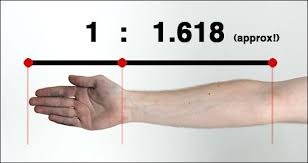
হাতের আঙ্গুলের হাড়ের দৈর্ঘ্যে সোনালী অনুপাত এবং ফিবোনাচ্চি নাম্বার দেখা যায়, এই ছবির মত:

এবার আমাদের আছে ২ হাত, প্রতি হাতে ৫ আঙ্গুল, ৮ আঙ্গুলে ৩ ভাগ করে, ১ আঙ্গুলে ২ ভাগ। এগুলো সব ফিবোনাচ্চি সংখ্যা!!

যাদের মুখের অবয়ব কে আমরা বলি নিখুঁত সুন্দর, দেখা গেছে তাঁদের নাক, চোখ, দাঁত, ঠোঁট- সব সোনালী অনুপাত মেনে চলে। দ্য ভিঞ্চির মোনালিসার ছবি বিশ্লেষণ করে দেখা গেছে, এটা সোনালী অনুপাত মেনে আঁকা হয়েছে। 

যে ঠোঁট সুন্দর, তা মেপে দেখা গেছে, উপরের ঠোঁট : নিচের ঠোঁট= ১:১.৬১৮।

জীবনের সমস্ত বৈশিষ্ট্য যে ডি এন এ অণু ধারণ করে, তার মধ্যেও দেখা যায় সোনালী অনুপাত। ডি এন এর এক প‍্যাচের  দৈর্ঘ্য  ৩৪ এঙস্ট্রম আর  প্রস্থ ২১ এঙস্ট্রম; এরা ফিবোনাচ্চি সংখ্যা, অনুপাত ১.৬১৯০...(১.৬১৮ এর চেয়ে ০.০০১ বেশী)। আবার তিন মাত্রার বিভিন্ন ভাইরাসের মধ্যেও সোনালী অনুপাত দেখা যায়।

ফুল- ফলেও সোনালী অনুপাত, ফিবোনাচ্চি সংখ্যা দেখা যায়। বেশিরভাগ ফুলের পাপড়ি দেখা গেছে ফিবোনাচ্চি সংখ্যা- পাঁচ, আট, একুশ, চৌত্রিশ এরকম,(অবশ্য এর কিছু কিছু ব্যতিক্রমও আছে)। সূর্যমুখী ফুলের মধ্যভাগে বিন‍্যস্ত  বিচির বিন্যাসে দুই ধরনের বাকা লাইন দেখা যায়। এক ধরনের লাইন ঘড়ির কাঁটার দিকে ঘুরে আরেক ধরনের লাইন বিপরীত দিকে।

গুনে দেখা গেছে দুদিকের লাইন সংখ্যা হয় ফিবোনাচ্চি সংখ্যা। আবার প্রতিটি লাইনে যে বিচিগুলো আছে সেগুলো ফিবোনাচ্চি সংখ্যা! আনারসেও ফিবোনাচ্চি সংখ্যা আছে, আমি প্রতিবার আনারস কাটার আগে গুনে দেখি। আনারসের চোখগুলো দুইদিকে বাঁকানো লাইন তৈরি করছে- ক্লক ওয়াইজ আর এ‍্যান্টি ক্লক ওয়াইজ। গুনলেই দেখা যায়, এক দিকে চোখের সংখ্যা ৮ আর অন্যদিকে চোখের সংখ্যা ১৩!! কোন কোন আনারসে অবশ্য সংখ্যাগুলো কখনও ৭ বা ১২ হয়, সেক্ষেত্রে দেখা যায় কোনো কোনো চোখ অপরিণত রয়ে গেছে।

পরীক্ষা প্রার্থনীয়।

অবশ্য, এই পরীক্ষা শুধু আনারস নিয়ে করে দেখাই  ভালো; নিজের নাক, চোখ, ঠোঁট মেপে অনুপাত বের করতে গেলে মন খারাপ হবার সম্ভাবনা  আছে।


সব ছবি: অন্তর্জাল

এই পোষ্ট লিখতে যেসব পোস্ট এর সাহায্য নেয়া হয়েছে, তার লিংক নিচে দেয়া হল:

১)
                            
২)

৩)

 https://www.livescience.com/37470-fibonacci-sequence.html 

 https://www.livescience.com/37704-phi-golden-ratio.html

 http://www.quran-m.com/firas/en1/index.php/human/409-the-golden-ratio.html

 https://en.wikipedia.org/wiki/List_of_works_designed_with_the_golden_ratio

 https://www.goldennumber.net/leonardo-da-vinci-golden-ratio-art/