ক্যালকুলাসে যতগুলো গানিতিক টার্ম আছে,তার মধ্যে সবচেয়ে পরিচিত টার্ম হচ্ছে 'লিমিট' বা 'সীমা'।মূলত এই লিমিটের কারনেই ক্যালকুলাস গণিতের অন্য শাখাগুলোর চেয়ে স্বতন্ত্র একটি তাৎপর্যপূর্ণ শাখায় পরিণত হয়েছে।সাধারন বীজগণিতের সাথে ক্যালকুলাসের মুল পার্থক্য মূলত এখানেই।যদিও লিমিটের পদ্ধতিগত রূপটি সাম্প্রতিককালে আবিষ্কৃত হয়,কিন্তু লিমিটের ধারনা ও ব্যাবহার অনেক পুরনো।প্রাচীন গ্রীসে বিভিন্ন অসম বস্তুর ক্ষেত্রফল ও আয়তন নির্ণয়ে সীমার আশ্রয় নেওয়া হতো।গ্রিক গণিতবিদ আর্কিমিডিস পাই এর মান বের করার জন্য যে ধারাটি প্রস্তাব করেছিলেন তার পিছনেও সীমার রহস্যময় প্রভাব লুকিয়ে ছিল।প্রসঙ্গত আর্কিমিডিসের ধারাটিঃ

যেখানে রুট এর নিচে n সংখ্যক 2 আছে।n এর মান যত বেশি হবে পাই এর মান তত নিখুত হবে।এ প্রসঙ্গে আমরা আবার পরে আসব।ভারতীয় অনেক গনিতবিদও সীমার পেছনে অনেক বড় বড় কাজ করেছেন।

এখন সীমা বলতে আসলে কি বোঝায় তা বোঝার একটা চেষ্টা চালাই।এর জন্য আমি একটি ফাংশন বিবেচনা করিঃ f(x)=(x^2+4x)/x. অনেকেই হয়ত আমাকে উপরোক্ত ফাংশনটি লিখতে দেখে বোকা ভাবছেন।হয়তোবা ভাবছেন লব থেকে x কমন নিয়ে হরের x এর সাথে কাটাকাটি করে ফেললেই তো ফাংশনটি কত সহজ হয়ে যায়। আসলেই কি তাই?দেখা যাক,আমরা উপরোক্ত ফাংশনটির জন্য input -output এর একটি chart তৈরি করিঃ

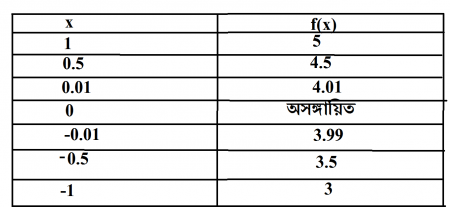
উপরের chart টি লক্ষ্য করলে,আমরা একটি বিষয় স্পষ্টভাবে দেখতে পাই,তা হচ্ছে: আমরা ধনাত্মক কিংবা ঋণাত্মক যেদিক থেকেই শূন্যের কাছাকাছি আসতে থাকি,সবসময়ই একটি সংজ্ঞায়িত output পাওয়া যায়।কিন্তু যেই আমি input হিসেবে শূন্য বসালাম,একটি ভয়ানক কাণ্ড ঘটে গেল; output পাওয়া গেল ০/০; যেটি কিনা গনিতের দৃষ্টিতে একটি প্রলয়ঙ্ককরী ব্যাপার।গনিত ০/০ এর মান উদ্ঘাটনে ব্যর্থ।যেটিকে গনিতের ভাষায় বলা হয় অনির্ণেয়।অধ্যাপক জাফর ইকবাল এ ব্যাপারটিকে উনার 'গনিতের মজা ,মজার গণিত'
বইয়ে খুব সুন্দরভাবে তুলে ধরেছেন এভাবেঃ

"গনিতে শূন্য দিয়ে ভাগ করার নিয়ম নেই।অর্থাৎ,কোথায় কেউ যদি কোনও কিছুকে শূন্য দিয়ে ভাগ করে তাহলে যা ঘটবে,গনিত তার কোনও দায়দায়িত্ব নেবে না"
কোনও সংখ্যাকে শূন্য দিয়ে ভাগ করা যায়না কেন ,তা বোঝা কঠিন কিছু না।যেমনঃ
আমরা জানি, 0=0 বা,0*1=0*100 ; এখন আমি যদি উভয়পক্ষকে 0 দিয়ে ভাগ দেই,তাহলে,শূন্য শূন্য কাটাকাটি গেলে আমরা পাবো 1=100 .চিন্তা করেছেন কি ভয়ানক ব্যাপার।যদি 1=100 হয় তাহলে যেকোনো সংখ্যা=যেকোনো সংখ্যা প্রমান করা যাবে।তাহলে গণিতের কোনও অর্থই থাকবে না।তাহলে সর্বোপরি কি বোঝা গেল?? লিমিট কিংবা সীমার মাঝেই ঘাপটি মেরে লুকিয়ে আছে অসীম।অর্থাৎ,সীমার মাঝেই অসীমের অবস্থান।(চলবে...)
পরবর্তী অংশ