১ম অংশের পর থেকে

মূলত এই অনির্ণেয়তার সমস্যা থেকেই লিমিটের আবির্ভাব ঘটেছে।যে সকল বিন্দুতে ফাংশনের মান সংজ্ঞায়িত নয়,সেইসব বিন্দুতেই মূলত লিমিট নির্ণয় করা হয়।এর কারন কি?চলুন এর কারন দেখার চেষ্টা করি।আমরা আগের পর্বে উল্লেখিত f(x)=(x^2+4x)/x ফাংশনটির জন্য তৈরি করা input-output এর chart টি আবারো নিচে উল্লেখ করিঃ

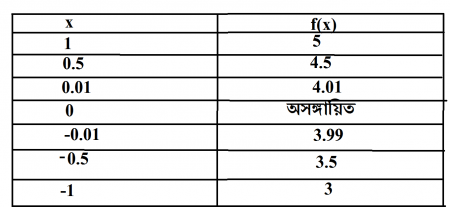
উপরের chart টির দিকে তাকালে দেখা যাবে,ফাংশনটিতে x এর মান শূন্য এর যত কাছাকাছি যেতে থাকে,f(x) এর মান ততই 4 এর কাছাকাছি যেতে থাকে।আমরা ধনাত্মক ও ঋণাত্মক যেদিক থেকেই শূন্য এর দিকে অগ্রসর হই না কেন,উভয় ক্ষেত্রে একই ঘটনা ঘটে,অর্থাৎ ফাংশনটি 4 এর কাছাকাছি যেতে থাকে।তাহলে আমরা বলতে পারি x=0 বিন্দুতে যদিও ফাংশনটি সংজ্ঞায়িত নয়,কিন্তু x=0 বিন্দুতে ফাংশনটির মান ঠিক কত হওয়ার প্রবণতা দেখায় তা আমরা লিমিটের সাহায্যে বের করতে পারি।তাহলে দেখা দেখা যাচ্ছে বিশেষ পরিস্থিতিতে 0/0 এরও একটি অর্থ আছে এবং 0/0 ঠিক কত হতে চায় তা ফাংশনের গঠনের উপর নির্ভর করবে।f(x) ফাংশনে x এর মান শূন্য হলে ফাংশনটি অনির্ণেয় হওয়ায়,শূন্য এর যথাসম্ভব কাছাকাছি মান নিয়ে আমরা x=0 বিন্দুতে f(x) এর মান সম্পর্কে একটি ধারণা নিতে পারি।নটর ডেম কলেজের গণিতের অধ্যাপক জহরলাল স্যার ব্যাপারটিকে আখ্যায়িত করেছেন এভাবেঃ

"দুধের স্বাদ ঘোলে মেটানো"

আমি বলেছিলাম x এর মান 0 এর কাছাকাছি যেতে থাকলে f(x) এর মান 4 এর দিকে এগোয়।কিন্তু একবার চিন্তা করে দেখুন তো x এর মান 0 এর কত কাছাকাছি যেতে পারে।এই ব্যাপারটি বলার আগে আমি নতুন আরেকটি টার্মের সাথে পাঠকদের পরিচয় করিয়ে দিতে চাইঃ"Infinitesimal" বা 'ক্ষুদ্রাতিক্ষুদ্র সংখ্যা'।সহজ করে বললে,Infinitesimal হচ্ছে 0 এর সবচাইতে কাছের সংখ্যা ।ব্যাপারটি কিন্তু এমন নয় যে,একটি নির্দিষ্ট সংখ্যা আছে যাকে infinitesimal বলে।আপনাকে যদি আমি শূন্য এর খুব কাছের একটি সংখ্যা লিখতে বলি ধরা যাক আপনি লিখলেন 0.000001;নিঃসন্দেহে খুব ছোট একটি সংখ্যা।কিন্তু এটিই কি 0 এর সবচেয়ে কাছের সংখ্যা?নিশ্চয়ই না।0.000000000001 নিশ্চয়ই তার চাইতেও ছোট;আবার0.00000000000000000000001 নিশ্চয়ই তার চাইতেও ছোট।এভাবে দেখানো যায় আপনি যে সংখ্যাটিই লিখবেন তার চাইতে ছোট আরেকটি সংখ্যা লিখা যাবে।আবার তার চাইতেও ছোট আরেকটি সংখ্যা থাকবে।একই কথা ঋণাত্মক সংখ্যার ক্ষেত্রেও প্রযোজ্য।-0.000001 শূন্য এর কাছের একটি সংখ্যা।কিন্তু এর চাইতে 0 এর কাছের ঋণাত্মক কি লিখা যাবে না।অবশ্যই যাবে!তাই কোনও নির্দিষ্ট সংখ্যাকে infinitesimal বলা যাবে না;infinitesimal মানে হচ্ছে কোনও সংখ্যার সাথে x এর কিংবা x এর সাথে কোনও সংখ্যার ব্যাবধান 0 এর সবচাইতে কাছের সংখ্যা ।এ কারনেই infinitesimal এর বাংলা অর্থ ক্ষুদ্রাতিক্ষুদ্র সংখ্যা,অর্থাৎ একটি ক্ষুদ্র সংখ্যার পরে আরেকটি ক্ষুদ্র সংখ্যা বিদ্যমান;আবার তার চাইতেও ক্ষুদ্র সংখ্যা বিদ্যমান।অর্থাৎ,আপনি যে সংখ্যাটিই লিখুন না কেন,infinitesimal তার চাইতেও ছোট সংখ্যা ।অর্থাৎ এটি খুবই ক্ষুদ্র সংখ্যা ;এত ক্ষুদ্র যে, যদি আমি একে শূন্যের সমান ধরে নেই,তাহলে পৃথিবীর কোনও ক্ষতি বৃদ্ধি হবে না। তাই আমাদের f(x) ফাংশনে এ x এর সাথে 0 এর ব্যাবধান এত ছোট হতে পারে যে, আমি যদি এটাকে 0 ধরে নেই , হিসাবে এক চুল পরিমাণও গড়মিল হবে না। আমাদের ফাংশনটির ক্ষেত্রে লিখলে আমার উপরের কথাগুলোকে ক্যালকুলাসের ভাষায় এভাবে লিখা হবেঃ

lim(x tends to 0) f(x)= lim (x tends to 0) (x^2+4x)/x

উপরের জটিল সমীকরণটি দেখে ভয় পাবার কিছু নেই। আস্তে আস্তে সব ব্যাখ্যা করছি।এখানে lim হচ্ছে লিমিট এর সংক্ষিপ্ত রূপ। lim এর নিচে x tends to 0.তার মানে হচ্ছে x,0 এর দিকে ধাবিত হচ্ছে কিংবা x ,0 এর সবচেয়ে কাছের সংখ্যা।limit এর সামনে রয়েছে f(x).অর্থাৎ যে ফাংশনটির লিমিট বের করতে হবে।সামগ্রিকভাবে এর অর্থ দাঁড়ায় x এর সীমা 0।অর্থাৎ উপরের সমীকরণটি আপনাকে সাবধান করে দিচ্ছে,'সাবধান, x যেন তার সীমা(0) লঙ্ঘন না করে।না হলে কেলেঙ্কারি বেধে যাবে'। বলা বাহুল্য, এই lim চিহ্নটির জনক হচ্ছেন ক্যালকুলাসের অন্যতম আবিষ্কারক 'গটিফ্রেড লিবনিজ'। তাহলে আমরা এখন

উপরোক্ত ফাংশনটিকে এভাবে লিখতে পারিঃ lim( x tends to 0 ) f(x)= lim( x tends to 0 ) (x^2+4x)/x = lim (x tends to 0)x(x+4)/x=lim (x tends to 0)(x+4)=0+4=4

তার মানে আমরা এখন হরের x ও লবের x কাটাকাটি করতে পারি।কারন,এখানে x tends to 0 ,but not equal 0.অর্থাৎ এখন x ,0 এর সবচাইতে কাছের সংখ্যা,কিন্তু 0 নয়।এভাবেই যেকোনো ফাংশনকে সুবিধাজনক অবস্থায় নিয়ে লিমিট নির্ণয় করা যায়। এবার যদি আমি উপরোক্ত ফাংশনের একটি লেখচিত্র আঁকার চেষ্টা করি তবে এরকম দেখাবেঃ

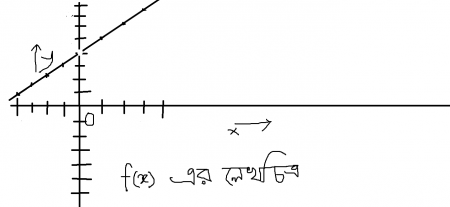
লেখচিত্রটি ভালো করে খেয়াল করলে দেখবেন ঠিক x=0 বিন্দুতে ফাংশনটির কোনও লেখ নেই।কারণটা বোঝা কঠিন কিছু না।আমরা ইতোমধ্যেই জেনে গেছি x=0 বিন্দুতে ফাংশনটি অনির্ণেয়।তাই বলা যায় ফাংশনটি x=0 বিন্দুতে বিচ্ছিন্ন।বিচ্ছিন্ন ও অবিচ্ছিন্ন ফাংশন কি তা সংক্ষিপ্তাকারে বোঝানো যাক।x এর সকল বাস্তব মানের জন্য কোনও ফাংশন সংজ্ঞায়িত হলে ,এর লেখচিত্রও x এর সকল বিন্দুতে অবিচ্ছিন্ন হবে।অন্যদিকে x এর কোনও মানের জন্য ফাংশনটি অসংগায়িত হলে,ঐ বিন্দুতে ফাংশনটি বিচ্ছিন্ন হবে।এ ব্যাপারে পরের কোনও পোস্টে বিস্তারিত আলাপ করা যাবে।লিমিটের মূল ব্যাপারটি সহজে বোঝানোর চেষ্টা করা হল।(চলবে...)