(কয়েকদিন আগে দু হাতের কব্জী রাস্তায় স্লিপ কেটে ফ্রাকচার হওয়ায় ব্যান্ডেজ লাগানো হইছে.. এই দু হাতে ব্যান্ডেজ নিয়েই এই লেখাটা লেখা! বানান ভুল বা বাক্য গঠনে সমস্যা হলে প্লিজ জানাবেন)

ডাইমেনশন বা মাত্রা নিয়ে যে কোনো প্রকারের কনফিউশন থাকলে এই ভিডিওটি দেখার অনুরোধ রইলো। সবাই বুঝে যাবেন ১০ মাত্রা কি! আজ থেকে কয়েকবছর আগেও এই ডি ব্রেন সম্পর্কে অনেক বাঘা বাঘা পদার্থবিদ মাথা চুলকাতো। আশা করি এই ভিডিও আপনাকেও একজন বাঘা পদার্থবিদ বানিয়ে দিতে পারে, তবে এই ভিডিও অনেক আগেই নেটে অনেকেই বহুবার শেয়ার করেছে।



আমার লেখার বিষয়বস্তু এত বিশদ নয়। তার আগে আমি একটু কথা বলি। আমরা ছোট বেলায় যখন পড়ালেখা শুরু করি তখন দেখতাম জ্যামিতিতে আমাদেরকে পড়ানো হতো x অক্ষ আর y অক্ষ। তারপর যখন আরও একটু পড়ালেখা করি তখন ছবি আকা বা যেকোনো বাক্স আকা শিখলে জানতে পারি আমাদের চারপাশে প্রতিটা দৃশ্যমান বস্তুর দৈর্ঘ্য, প্রস্থ এবং উচ্চতা বর্তমান। এখন আপনি হাত উচিয়ে বলতে পারেন একটা কাগজের তো শুধু দৈর্ঘ্য প্রস্থ আছে কিন্তু উচ্চতা তো নেই।

কথাটা ঠিক আবার ঠিক না। ঠিক এই জন্য যে আপাত দৃষ্টিতে এর কোনো উচ্চতা নাই কিন্তু আবার বেঠিক এই জন্য যে এই কাগজটা কত মোটা সেটা যত সূক্ষ্মই হোক সেটাই উচ্চতা।

তো আমরা ধরে নেই তার কোনো উচ্চতা নেই। তার মানে ফিনফিনে কাগজটার মাত্র দুটো মাত্রা কিন্তু যখন এটা দিয়ে কোনো বাক্স বানান বা শুধু ভাজ করেন তাহলে আপনি এর একটা উচ্চতা পাবেন।

এটা গেলো বাস্তবতার ভিত্তিতে। এখন ডাইমেনশন নিয়ে যখন চিন্তা ভাবনা শুরু হয় তখন দেখা যায় গানিতিক ভাবে উচ্চতর মাত্রা দিয়ে বস্তুর জ্যামিতিক গঠন কি হতে পারে সেটা অনুমান করা খুব কঠিন কিছু না। আপনি গানিতিক ভাবে চোখ বুঝে ঘাত সমূহের ইন্টিগ্রাল ইকোয়েশন দিয়ে তাদের জটিল ফিগার গুলোর জিওম্যাট্রিক রূপ দিতে পারেন।

কিন্তু আপনি যখন পদার্থবিজ্ঞানের মৌলিক তত্বে আসবেন তখন একটু সমস্যা। এই যেমন আপনি বস্তুর দৈর্ঘ্য প্রস্থ আর উচ্চতা দেখছেন, এর পর কি?চিন্তা করেন।

যদি আমরা এই দৈর্ঘ্য প্রস্থ উচ্চতাকে জ্যামিতি অনুসারে আকি তাহলে নীচের ছবির মতোই মনে হবে যা x, y , z দিয়ে ব্যাখ্যা করা যায়।

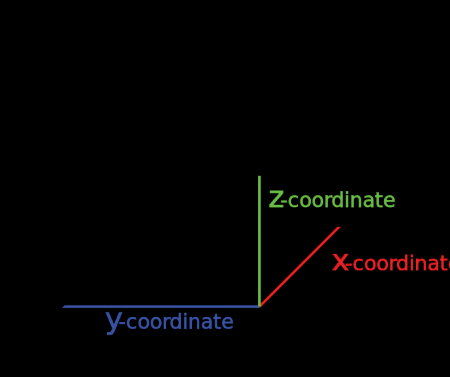
চিত্র ১: এখানে এই বাক্সটির দৈর্ঘ্য প্রস্থ এবং উচ্চতা দুটোই বিদ্যমান। গানিতিক ভাবে যেটাকে আমরা x,y,z ভাবে বলতে পারি।

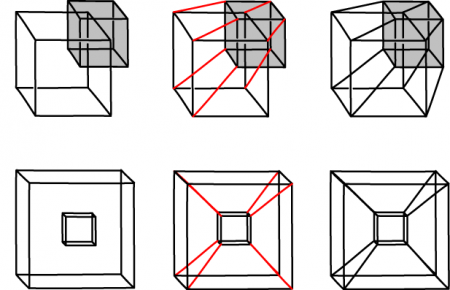
চিত্র ২: এখানে x,y,z ছাড়াও আরেকটা মাত্রা আছে যার ফলে ছবিটাএরকম হয়েছে। আসলে স্থানিক মাত্রাগুলো সবসময় একটার ওপর লম্বভাবে (৯০ ডিগ্রি কোনে) অবস্থান করে কিন্তু এর দিক থাকবে ভিন্ন। তাই বাক্স পেটে ঢুকে গেছে। সূত্র: Click This Link


আইনস্টাইন যখন স্পেশাল থিওরী অব রিলেটিভিটি নিয়ে দুনিয়া মাতাচ্ছিলো তখনও মহাবিশ্বের মৌলিক বলের চারটির সবকয়টি আবিষ্কার হয় নি। দুর্বল এবং শক্তিশালী মিথস্ক্রিয় বল সম্পর্কে তখন কোনো আইডিয়া ছিলো না। তবে আইনস্টাইনের মাথায় এটা ঘুরছিলো যে মৌলিক যত বল (তড়িৎচৌম্বকীয় বল আর গ্রাভিটি) এগুলোকে কিভাবে একীভূত করা যায়। যদি এগুলো একীভূত করাই যায় তাহলে মহাবিশ্ব সৃষ্টির সকল প্রশ্নের উত্তর পাওয়া যাবে বৈকি। কিন্তু কোনো ভাবেই এই বল দুটিকে একীভূত করা যাচ্ছিলো।

আইনস্টাইনের স্পেশাল থিওরী অব রিলেটিভিটি অনুসারে যেকোনো ভর বিশিস্ট বস্তু কোথাও অবস্থান করে সেখানে স্থান কালের মাত্রা বেঁকে যায়। এর সবচেয়ে বড় প্রমান হলো গ্রাভিটেশনাল লেন্সিং যেটা আমরা মহাবিশ্বকে টেলিস্কোপ দিয়ে কোনো বিশাল তারা বা ব্লাক হোলকে অনুসরন করলে দেখা যাবে তার পাশ দিয়ে আলো বেকে যাচ্ছে। আলো হচ্ছে একটি তড়িৎচৌম্বকীয় বল যার গতিবেগ আমাদের জানা মতে সর্বোচ্চ।

তো আইনস্টাইনের এই তত্বে স্থান কাল মাত্রার হিসাব ৪ মানে ৪ টি মাত্রা বিদ্যমান যার তিনটি হলো স্থানিক মানে দৈর্ঘ্য প্রস্থ উচ্চতার সমমান এবং আরেকটি হচ্ছে সময় মানে আলোর গতি অথবা যেভাবে আপনি ইন্টারপ্রেট করেন (এটা করা হয়েছে গানিতিক ব্যাখ্যার সাথে সহজে মেলানোর জন্য)।

কালুজা ক্লেইন থিওরী:

আইনস্টাইনের স্থান-কাল নিয়ে স্পেশাল থিওরী অব রিলেটিভিট যখন সবাইকে চমকে দিলো তখন কালুজা-ক্লেইন নামের দুই গনিতবিদ ভাবলেন যে স্থানিক এই তিনমাত্রা ছাড়াও যদি আরও একটি মাত্রা থাকে তাহলে কি হবে...

আইনস্টাইনের স্পেশাল রিলেটিভিটি অনুযায়ী আমরা একটা ধারনা পাই স্থান-কালের মাত্রা কোনো ভরের উপস্থিতিতে বেকে যেতে পারে। যেমন আপাত দৃস্টিতে ধরা যাক আমাদের পৃথিবী পৃষ্ঠ বাকানো মানে পুরাই গোলাকার। পৃথিবীপৃষ্ঠের যেকোনো বস্তুর অবস্থান জানতে আমরা ব্যাব হার করি অক্ষাংশ এবং দ্রাঘিমাংশ। কিন্তু এই মাত্রা দুটো পর্যায়ক্রমিক কারন আপনি যদি পৃথিবীর এক বিন্দু থেকে হাটা শুরু করেন সোজাসুজি তাহলে পুরো পৃথিবী ঘুরে সেই বিন্দুতেই চলে আসবেন। তার মানে পৃথিবীপৃষ্ঠটি আমাদের পারিপার্শ্বিক তিন মাত্রার জগতে একটা দ্বিমাত্রিক তল। ঠিক যেমন আপনার রুমের মেঝেতে পড়ে আছে একটা পাতলা সিলিন্ডারের মতো দু পাশের প্রান্ত আটকানো কাগজ।

কালুজা-ক্লেইন ভাবলেন যে যদি আমাদের বাহ্যিক মাত্রাগুলোর মধ্যে কোনো এক মাত্রা এমন ভাবে বাকানো হয় তাহলে কি হবে? ঐ বাকানো মাত্রাটি এভাবে চিরদিন চলতে পারে না কিন্তু ঐ বাকানো মাত্রার কারনে পুরো স্থান বা বস্তুটি একটি বৃত্তের সৃষ্টি করবে। স হজ ভাষায় আপনি হাতে কাগজ নিন। এর দৈর্ঘ্য আর প্রস্থ পাবেন। এখন আপনি দৈর্ঘ্য বা প্রস্থ বরাবর দুই প্রান্ত এক করেন তাহলে কি গোলাকার সিলিন্ডারের আকার নিচ্ছে না? সেরকম ভাবে বোঝার সাথে একটা চ্যাপ্টা বাক্স নিন যার দৈর্ঘ্য প্রস্থ এবং উচ্চতা তিনটাই পাবেন। এখন আপনি তার দৈর্ঘ্য বা প্রস্থ বা উচ্চতা যেকোনো মাত্রা বরাবর বাকিয়ে দুই প্রান্ত লাগিয়ে দিন, বাক্সটি কি গোলাকার হবে না? তাহলে আপনি দেখতে পাবেন ঐ সিলিন্ডার আকৃতির কাগজ বা বাক্সের পৃষ্ঠে যেভাবেই হোক একটা দাগ টানা শুরু করলে তার শেষ হবে ঐ দাগের শুরুর বিন্দুতে। তাহলে আপনি পেয়ে গেলেন বাকানো মাত্রা সমূহ।

তবে এই বক্রাকৃতির অবস্থা নির্ভর করবে আপনি কোন মাত্রাটাকে বাকিয়েছেন। যদি বৃত্তটির সাইজ একটা এটমের লক্ষ কোটি ভাগের এক ভাগ হয় তাহলে এই বক্র মাত্রাটি আপনার চোখে ধরা পড়বে না। তেমন ভাবেই আপনি একটা কাগজ নিয়ে ছোটবেলার সেই খেলার মতো এই কোনো ধরে যত ক্ষুদ্র সম্ভব গোলকরে ফেললেন তাহলে দেখা যাবে গোলাকার কাগজটি পাইপের মতো লম্বা হবে কিন্তু এর বক্রাকৃতির ব্যাস খুব কম থাকায় দূর থেকে একে আপনার একটি সরল রেখাই মনে হবে। ঠিক এই জিনিসটাই মাত্রার ক্ষেত্রে ভেবে দেখেন তাহলে ঐ বক্রাকৃতির বল আপনার কাছে নগন্যই মনে হবে। কালুজা এবং ক্লেইন ঠিক এই কনসেপ্ট নিয়েই গনিত কষে দেখালেন যে আপনার ত্রিমাত্রিক জগতের ভেতর আরেকটা ছোট মাত্রা থাকতে পারে এবং সেটি যদি এমন অতিক্ষুদ্র ব্যাসার্ধের হয় যেটা ধরতে পারেন প্লাংকের স্কেলে মাপতে হবে, তাহলে সেটা আপনার অনুভূতির বাইরে।

তখন সবাই ভাবতে লাগলেন এই অতি ক্ষুদ্র চতুর্থ মাত্রা যেটা আমার গায়েই লাগে না সেটা নিয়ে ভাববো কেন? তখন কালুজা-ক্লেইন দেখালেন জেনারেল রিলেটিভিটির মাধ্যমে যে এই অতিরিক্ত মাত্রা আমাদের ওপর তারপরও কিছু প্রভাব ফেলে যেমনটা ফেলে গ্রাভিটি নামের বলটি। এবং গ্রাভিটির তুলনায় তড়িৎচৌম্বকীয় বল ততটাই শক্তিশালী। তাহলে দেখা গেলো আমরা স্থানিক তিন মাত্রা পেলাম, বাকানো অতিক্ষুদ্র মাত্রা হিসেবে গ্রাভিটিকে এবং ৫ নম্বর মাত্রা হলো তড়িৎচৌম্বকীয় বল যাকে আলো হিসেবে ধরে হিসাব করতে পদার্থবিদেরা পছন্দ করেন এবং আইনস্টাইনের রিলেটিভিটির তত্ব আর হাইপোতে আলোকেই সময়ের সম্পর্কযুক্ত ভাইরা ভাই তুলে ধরেছেন।
সূত্র

এই তত্বে গানিতিক ভুল না থাকলেও যখন পদার্থবিজ্ঞানে এর প্রয়োগ ঘটানো হয় তখন দেখা যায় এই হিসেবে ইলক্ট্রনের ভরের বেশ হের ফের ঘটে। মানে পরীক্ষিতভাবে যে ভর পাওয়া যায় তার চেয়ে ব হুগুন বেশী পার্থক্য থেকে যায়। এছাড়া এই তত্ব শুধু তড়িৎচৌম্বকীয় বল এবং গ্রাভিটিকে নিয়ে কাজ করে কিন্তু পরবর্তীতে আবিস্কৃত হওয়া বাকি দুটো মৌলিক বল: দুর্বল এবং শক্তিশালী মিথস্ক্রিয় বলকে একীভূত করাটা সম্ভব হয় নাই।

তার ওপর দেখা যায় এই বাকানো মাত্রার কারনে পুরো বস্তুটি গোলাকার হয়েই যায় তাহলে তার পৃষ্ঠ বরাবর তড়িৎচৌম্বকীয় বলপ্রাপ্ত কনিকা সমুহ পরিভ্রমন করবে।যদি ইলেক্ট্রনের কথা চিন্তা করি, এই বাকানো মাত্রার ব্যাসার্ধ ইলেক্ট্রনের তড়িৎচার্জের সাথে সম্পর্কযুক্ত এবং যখন পৃষ্ঠে বরাবর ইলেক্ট্রন ঘুরা আরম্ভ করবে তাহলে অপর দিকে এর এন্টি ইলেক্ট্রন মানে পজিট্রনও ঘুরবে এবং একটা বিন্দুতে এসে তাদের সংঘর্ষ হয়ে তারা ধ্বংস হয়ে যাবে। যেটা বাস্তবে হচ্ছে না। পৃথিবী থেকে নিঃসরিত আলো বা সূর্য্য পৃষ্ঠের বিকিরন নিঃসরিত হয়ে সরলপথেই গমন করছে.....কিছুই ধ্বংস হচ্ছে না।

আইনস্টাইন তার শেষ জীবনে সকল বল একীভূত করনের কাজ হাতে নিলেন তখন তার সামনে সবচেয়ে ভালো এবং কার্যকরী তত্ব ছিলো এই থিওরীই। কিন্তু এই কাজটি শেষ করার আগেই তিনি মারা যান। পরে যখন স্ট্রিং থিওরী এসে বললো শুধু ৫ টা না, ঐ তিনটা স্থানিক মাত্রা আর কালের মাত্রা বাদের প্রায় সবই বাকানো মাত্রা, তখন অনেকটা এই সমস্যার সমাধান হয় কিন্তু সেখানে আরো বেশ কিছু সমস্যার উদয় হয় সেটা হলো এলএইচসিতে এই পর্যন্ত যতগুলো কলিশন ঘটানো হইছে তার কোনোটাতেই স্ট্রিং থিওরীকে সমর্থন দেবার মতো কোনো কনিকা পাওয়া যায়নি।

আপনি হয়তো বলতে পারেন যেহেতু এসব কনিকার ভর কাল্পনিক এবং গতি আলোর খুব কাছাকাছি বা বেশী তাহলে এলএইচসি পাবে কিভাবে? এলএইচসিতে এই পর্যন্ত ১৪ টেরাইলেক্ট্রন ভোল্টের নীচে এি সংঘর্ষ ঘটানো হয়েছে এবং যদি এইসব কনিকা থেকেই থাকে তাহলে এসব কনিকা যে ভর নিয়ে তৈরী হবে সে ভর নিয়ে তারা অন্য মাত্রায় উধাও হয়ে যাবে। তার মানে আপনি যদি ৭ টেরা ইলেক্ট্রনভোল্ট দিয়ে কোনো কলিশন ঘটান তাহলে কলিশনের পর ৭ টেরাভোল্টের হিসাব পাবেন না। এর বেশ কিছু অংশ উধাও হয়ে যাবার কথা। কিন্তু তা হয় নি।

যদিও স্ট্রিং থিওরির লোকজন এর কারন হিসেবে হাইয়ারার্কি প্রবলেমের কথা বলে!

গ্রাভিটেশনাল ওয়েভ:

প্রথমে আমাদের বুঝতে হবে এই স্পেস টাইমটা কি? তাহলে চলেন আমরা একটা বিশাল পুস্কুরিনি দেখতে যাই। আমি যখন ঢাকা ছাড়ি শেষবারের মতো তখন ঢাকা শহরে পুস্কুরিনী খোঁজা আর খড়ের গাঁদায় সুই খোজা এক কথা। পুরা ঢাকা শহর যেনো ইটের দালানো বস্তি। যাই হোক ধরে নিলাম আপনি গ্রামের কোনো বিশাল পুস্কুরিনিতে বসে আছে যেটা খুব শান্ত। কোনো ঢেউ নেই। এখন আপনি তার মাঝখানে একটা ঢিল ছুড়েন তাহলে কি হবে? একটা ঢেউয়ের সৃষ্টি হবে।

বিগব্যাং বা যে মহাবিস্ফোরনের কারনে এই মহাবিশ্বের জন্ম এর গোড়া থেকেই শুরু হয়েছে স্হান কাল মাত্রার প্রসারন। সোজা কথায় সময় এবং স্থানের পথ চলা। আমাদের পুকুরের পানির শান্ত পৃষ্ঠটাই হলো এই স্পেস টাইম এবং যখনই আপনি এর মধ্যে ভর যুক্ত কলেন তখনই এই স্থান কাল বেকে যায়। এটা আইনস্টাইনের স্পেশাল রিলেটিভিটি থেকে জানতে পারি। কিন্তু যখন একটা ঘুরা শুরু করে তখন দূরের বস্তুকে আকর্ষন করতে শুরু করে যেটাকে আমরা গ্রাভিটি বলতে পারি।

অনেকটা আপনি একটা গ্লাসে পানি নিয়ে চিনি ঢাললেন এবং চামচ ডুবিয়ে নাড়াতে শুরু করলেন। দেখবেন পানিতে একটা ঘূর্নীর সৃষ্টি হয়েছে এবং মাঝখানে ডেবে গিয়ে এক কেন্দ্রে গিয়ে মিশছে কেন্দ্রমুখী বলের কারনে। এখন যদি গ্লাসের এক প্রান্তে কোনো কাগজের ছোট টুকরা ফেলেন তাহলে সেটিকেও কেন্দ্রে আকর্ষন করবে। ঠিক এমনটিই ঘটছে সূর্য্য এবং তার গ্রহের ক্ষেত্রে আর এই যে স্থান কালের পৃষ্ঠে যে ঢেউ এটাই হলো গ্রাভিটেশনাল ওয়েভ এবং এটি সময়ের গতিতে চলে।

বিজ্ঞানীরা এই গ্রাভিটেশনাল ওয়েভের এফেক্ট ধরতে পেরেছেন তাদের লিগো এক্সপেরিমেন্ট সেন্টারে যেটাতে মূলত শক্তিশালী গ্রাভিটেশনাল ওয়েভের কারনে সৃষ্ট স্থানিক যে সংকোচন হয়েছে সেটাকে নির্নয় করেছে এবং এর মান হলো একটি প্রোটনের ব্যাসার্ধের সমান।

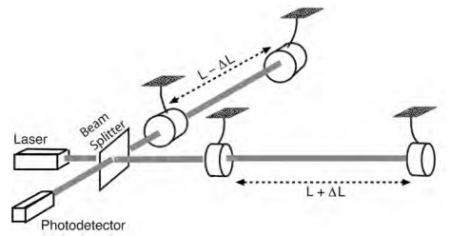
চিত্র ৩: লিগোর বেসিক ডায়াগ্রাম।

এখন কথা হলো দুইটা ব্লাক হোলের সংঘর্ষ অনেক বড় ব্যাপার এর বাইরে কি গ্রাভিটেশনাল ওয়েভ হয় না? অবশ্যই হয়। আপনারা স্বামী স্ত্রী দুজনে মিলে নাচলেও হয় কিন্তু তার মান এত কম যে সেটা ডিটেক্ট করা যায় না। কারন গ্রাভিটি নিজেই খুব দুর্বল।

এই ব্যাপারে ডিটেলস লেখার ইচ্ছে ছিলো কিন্তু পত্র পত্রিকায় ব্লগ সমূহতে এতো লেখা হয়েছে এই নিয়ে যে আর কিছু লেখার ইচ্ছে নাই।

তবে এটা নিয়ে যে কথা না বললেই নয় সেটা নিয়ে আলোচনা করবো।

মিশিও কাকু এর মধ্যে ডিক্লেয়ার দিয়ে দিছেন যে টাইম মেশিন বানানোতে এখন তত্বগত কোনো বাধা নেই, যে বাধা আছে সেটা হলো প্রকৌশল গত। মানে ইন্জ্ঞিনিয়ারগুলান কাম পারে না দেইখা টাইম মেশিন আবিস্কার হইতেছে না!

উনাকে কিছু বলার নাই, সারা জীবন ফিজিক্স বেচে অনেক কিছু করছেন, কিন্তু এভাবে প্রকৌশলীদের ওপর দোষারোপ করা তার বিমাতাসুলভ আচরনের মধ্যেই পড়ে! (কিডিং)


গ্রাভিটেশনাল ওয়েভ এবং টাইম মেশিন:


যখন বিগ ব্যাং ঘটেছিলো তখন থেকেই এই সময় আর স্থানের মাত্রা শুরু। বিস্ফোরনের ১ সেকেন্ডের অতি ক্ষুদ্র সময় (প্লাংক টাইম= ১০^-৪৩ সেকেন্ড) পর্যন্ত ৪ টি মৌলিক বল (গ্রাভিটি, তড়িৎ চৌম্বকীয়, দুর্বল মিথস্ক্রিয়, শক্তিশালী মিথস্ক্রিয় বল) একত্রেই ছিলো (যেখানে গ্রাভিটিই ছিলো সবচেয়ে শক্তিশালী এবং কর্তৃত্ব পরায়ন), এর পরই শুরু হয় ইনফ্লেশন....তারপর সবাই জানেন হয়তো। কথা হলো এই বিস্ফোরনের ফলে একটা শক্তিশালী গ্রাভিটেশনাল ওয়েভের সৃষ্টি হয়েছিলো এবং এটা এখনও এই মহাবিশ্বে বিদ্যমান। মহাবিশ্বে পরিভ্রমন কালে এরকম আরও বিস্ফোরনের কারনে এটা আরো শক্তিশালী হয়েছে এবং এর মধ্যে যে অতিআদি বিস্ফোরনের যে চিহ্ন সেটাও ব হন করছে যদিও সেটা অনেকটা বিকৃত।

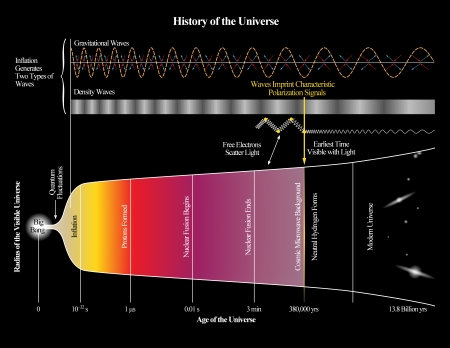
চিত্র ৪: বিগ ব্যাং এর ক্রোনোলজিক্যাল ধারা।

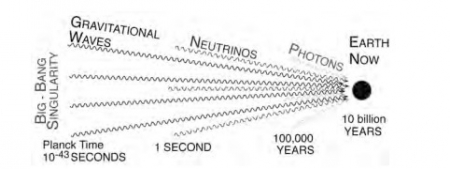
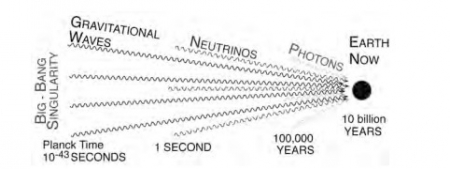
চিত্র ৫: বিগ ব্যাং এর পর গ্রাভিটেশনাল ওয়েভ ভ্রমন করে পৃথিবী পর্যন্ত পৌছাতে যা সময় লাগতে পারে।

আমরা এখন থেকে মহাবিশ্বের দিকে তাকাবো তখন আমরা গ্রাভিটির কারনে আলোর যে গতির যে পরিবর্তন যার ফলে দূরবর্তী ঘটনায় কি ঘটেছে, সেখানে স্থানিক মাত্রার কি পরিবর্তন সাধিত হয়েছে সেটা সম্পর্কে একটা পরিষ্কার ধারনা পেতে পারি। এছাড়া এই গ্রাভিটেশনাল ওয়েভের অস্তিত্ব আইনস্টাইনের স্পেশাল রিলেটিভিটির একটা গুরুত্বপূর্ন দিকো প্রমান করে যেটা আসলে পৃথিবীতে কোনো ল্যাবে প্রমান করা সম্ভব নয়।

আরেকটা ব্যাপার হতে পারে সেটা হলো জিপিএস সিস্টেম আরো নিখুতভাবে কাজ করতে পারে। তখন হয়তো জিপিএস গাইডেড গুলি ডিজাইন করা যাবে যে গুলিটা দেখা গেলো মঙ্গলবারের ভরা বাজারে ১০০০ লোকের সাথে দাড়িয়ে থাকা মোল্লা হামিদ চাচা কপালের মাঝখানে বিধে যাবে খুবই নিখুত ভাবে!

তবে এর সাথে টাইম মেশিনের সম্পর্ক এটাই থাকতে পারে যে গ্রাভিটির কারনে স্থানের সংকোচন বা প্রসারন ঘটে তার ফলে স্থানের মাত্রার বিকৃতি ঘটে। এখন কথা আসে গ্রাভিটি যদি সত্যি আলাদা মাত্রা হয় তাহলে এটা কি স্থানিক মাত্রা সমূহকে বাকাতে পারবে? যদি পারে তাহলে তড়িৎচৌম্বকীয় বল বা আলো যে স্থান থেকে যাত্রা শুরু করেছে সে স্থানে ফিরে আসবে? (কিন্তু এখানে তো ঐ সমস্যা: কালুজা ক্লেইনের ক্যালকুলেশন অনুযায়ী ইলেক্ট্রন আর পজিট্রন গোলাকার পথে হাটা দিলো দু দিকে, তারা পৃষ্ঠ বরাবর ভ্রমন করে নিজেদের সাথে সংঘর্ষ করলে শেষ, তো?)

এগুলোর সমাধান করা গেলে তবেই বোঝা যাবে গোডলের ক্লোজড টাইম কার্ভেচার তৈরী হবে কিনা। তার আগে চার বলের একীভূত করন মানে theory of everything প্রমান করা দরকার!

তাই টাইম মেশিনের সাথে এই গ্রাভিটেশনাল ওয়েভের সম্পর্ক এমন যে আমি সিগারেট খাচ্ছি তাই এন্টার্কটিকার বরফ গলছে। এই কথাটা আপনার কাছে যেমন হাসির খোড়াক দেবে, আবার কোনো কিছুর সাথে কোনো কিছু সম্পর্কযুক্ত না এটা ভাবাটাও বাতুলতা!

লেখাটি লিখতে অনুরোধ করেছেন জনৈক কৃষ্ঞচূড়া!