০,১,১,২,৩,৫,৮,১৩,২১,............... ফিবোনাচ্চি ক্রম

২৪ শে এপ্রিল, ২০০৯ সন্ধ্যা ৬:৩৩

আমি ফিবোনাচ্চি সিরিজটি সম্বন্ধে প্রথম জানতে পারি দ্যা ভিঞ্চি কোড বইটি পড়ে। তখনই সিরিজটির প্রতি বেশ আগ্রহ জন্মে। কিন্তু তখন বাসায় নেট ছিল না। তাই এই সম্বন্ধে বেশী জানতে পারি নি। এক ভাইয়াকে জিজ্ঞাসা করলে উনি প্রাথমিক একটা ধারনা দিয়েছিলেন ফিবোনাচ্চি সিরিজ সম্বন্ধে । পরবর্তীতে হুমায়ুন আহমেদ এর সায়েন্স ফিকশন “শূণ্য”তেও এর উল্লেখ পাই। তখন আবার পুরোনো আগ্রহ জন্মে ফিবোনাচ্চি সংখ্যার উপর। তাছাড়া আমাদের “ডিসক্রিট ম্যাথ” এর সিলেবাসে ফিবোনাচ্চি সিরিজ থাকায় সেই সময় এর বেশ খানিকটা পড়াশুনার সুযোগ হয়। তাই নিয়েই লিখছিঃ



ফিবোনাচ্চি সিরিজটির নামকরণ করা হয়েছে এর আবিষ্কর্তা লিওনার্দো ফিবোনাচ্চির নামে। তাকে মধ্যযুগের অন্যতম শ্রেষ্ঠ গণিতবিদ হিসাবে ধরা হয়। ফিবোনাচ্চি রাশিমালা শুধুমাত্র গণিত নয় বরং প্রকৃতিরও অনেক রহস্যে উন্মোচন ঘটাতে সক্ষম বলে অনেকের ধারণা। এই ব্যাপারে ফিবোনাচ্চি নিজেই বলে গেছেনঃ "প্রকৃতির মূল রহস্য এই রাশিমালায় আছে”। সিরিজটি হল এই রকমঃ

০,১,১,২,৩,৫,৮,১৩,২১,৩৪,৫৫,৮৯,১৪৪,২৩৩,৩৭৭, … …

এই সিরিজটির বৈশিষ্ট্য হলঃ

১. এই সিরিজের যে কোন সংখ্যা তার পূর্ববর্তী দুটি সংখ্যার যোগফলের সমান।
যেমনঃ ০+১=১
১+১=২,
২+১=৩,
৩+২=৫,
৫+৩ =৮, … … … ইত্যাদি।
গাণিতিক রাশিমালার সাহায্যে বলা যায়ঃ F(n)=F(n-1)+F(n-2); যেখানে F(0)=0 এবং F(1)=1 । ঠিক বিপরীতভাবে যেকোন সংখ্যা তার পরবর্তী দুটি সংখ্যার বিয়োগফলের সমান।

২. এই সিরিজের যেকোন ৪টি সংখ্যা নেয়া হলে ১ম ও ৪র্থ সংখ্যার যোগফল থেকে ২য় ও ৩য় সংখ্যার যোগফল বিয়োগ দিলে সবসময় ওই ৪ট সংখ্যার ১ম টি পাওয়া যাবে। আবার ১ম ও ৪র্থ সংখ্যার গুনফল থেকে ২য় ও ৩য় সংখ্যার গুনফল বিয়োগ দিলে সবসময় বিয়োগফল ক্রমান্ব্য়ে ১ এবং -১।
যেমনঃ আমরা ফিবোনাচ্চি সিরিজ থেকে যেকোন ৪টি সংখ্যা নিলামঃ ৫,৮,১৩,২১। এখন এর মাঝেঃ

১ম ও ৪র্থ সংখ্যার যোগফল= ৫+২১=২৬
২য় ও ৩য় যোগফল= ৮+১৩=২১
বিয়োগফল= ২৬-২১=৫(ওই ৪টি সংখ্যার ১ম সংখ্যা)

১ম ও ৪র্থ সংখ্যার গুনফল= ৫*২১=১০৫
২য় ও ৩য় সংখ্যার গুনফল= ৮*১৩=১০৪
বিয়োগফল= ১০৫-১০৪=১
আবার পরের চারটি মানে ৮,১৩,২১,৩৪ এর জন্য হিসাব করে দেখুন এক্ষেত্রে বিয়োগফল পাবেন -১। বিশ্বাস না হলে মিলেয়ে দেখুন।

৩. এবার ফিবোনাচ্চি সিরিজের মজার একটি বৈশিষ্ট্যে যাই, সবগুলি সংখ্যার শেষ ডিজিটে যেই নাম্বার গুলো আছে সেগুলো খেয়াল করুনঃ
০,১,১,২,৩,৫,৮,১৩,২১,৩৪,৫৫,৮৯,১৪৪,২৩৩,৩৭৭,৬১০,৯৮৭,……………….
সেই ডিজিটগুলো আলাদা করিঃ
৩,১,৪,৫,৯,৪,৩,৭,০,৭,……………………
মিলিয়ে দেখুন এরাও ফিবোনাচ্চি ক্রমে আছে।এবং এরাও আগের বৈশিষ্ট্য অনুসরণ করে। এক্ষেত্রে যদি পূর্ববর্তী দুটি সংখ্যার যোগফল একের অধিক বা দুই ডিজিটের হয় তবে তার শেষ ডিজিট আসবে। ফিবোনাচ্চি সিরিজের প্রতি ৬০টি সংখ্যার পর এই ডিজিটগুলো আবার রিপিট করে। যেমন ফিবোনাচ্চি সিরিজের
৬০ তম সংখ্যা= ১৫৪৮০০৮৭৫৫৯২০
৬১ তম সংখ্যা= ২৫০৪৭৮০৭৮১৯৬১
৬২ তম সংখ্যা= ৪০৫২৭৩৯৫৩৭৮৮১
৬৩ তম সংখ্যা= ৬৫৫৭৪৭০৩১৯৮৪২
৬৪ তম সংখ্যা= ১০৬১০২০৯৮৫৭৭২৩
৬৫ তম সংখ্যা= ১৭১৬৭৬৮০১৭৭৫৬৫

মজার ব্যাপার হল একইভাবে ফিবোনাচ্চি সিরিজের প্রতিটি সংখ্যার শেষ দুই ডিজিট, শেষ তিন ডিজিট ,চার ডিজিট এরকম করে সব ডিজিটের এর মাঝেই ফিবোনাচ্চি সংখ্যার বৈশিষ্ট্যগুলো খুজে পাওয়া যায়। বিশ্বাস না হলে সব গুলো সংখ্যার জন্য মিলিয়ে দেখুন। এই সিরিজের প্রায় ৩০০টি সংখ্যা পাবেন এই লিঙ্ক এঃ Click This Link


৪. এখন আমরা কয়েকটি ফিবোনাচ্চি সংখ্যার ভাগ করে দেখিঃ ২/১=২
৩/২=১.৫
৫/৩=১.৬৬৭
৮/৫=১.৬
১৩/৮=১.৬২৫
২১/১৩=১.৬১৫

অর্থাৎ প্রথম দুটি ভাগফল বাদ দিলে বাকি ভাগফলগুলোর মান প্রায় সমান বা ধ্রুবক। এই ধ্রুবক সংখ্যাটি "সোনালী অনুপাত" বা "স্বর্গীয় অনুপাত", ইংরেজীতে"Giolden Ratio " নামে পরিচিত। সোনালী অনুপাত বা স্বর্গীয় অনুপাত 'ফাই'(phi) দ্বারা প্রকাশ করা হয়। এর মান ১.৬১৮০৩৩৯৮৯ (প্রায়)। একে স্বর্গীয় অনুপাত বলার কারন হল মানবদেহের কয়েকটি অংশের অনুপাতের সাথে এর মিলে যাওয়া।যেমনঃ

* আমাদের forearm এর সাথে হাত এর অনুপাতের মান হল ১.৬১৮
* আমাদের মুখের দৈর্ঘ্যের সাথে নাকের প্রস্থের অনুপাত ১.৬১৮
* আমাদের fingertip থেকে এলবোর দৈর্ঘ্য এবং কবজি থেকে এলবোর দৈর্ঘ্যের অনুপাত ১.৬১৮

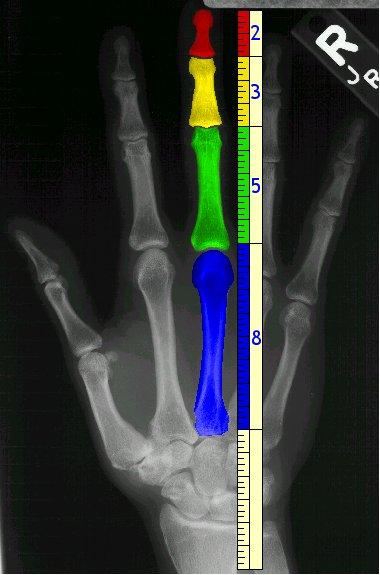
৫. আমাদের দেহের বিভিন্ন অংশে ফিবোনাচ্চির বেশ কিছু ক্রম পাওয়া যায়। আগের তিনটি উদাহরন তো দিলামঃ নিচে আমাদের মধ্যমার হাড়্গুলোর একটি ছবি দিলামঃ খেয়াল করে দেখুনঃ


এই হাড়গুলোর দৈর্ঘ্য ফিবোনাচ্চি সংখ্যার ক্রম। তাছাড়া আমাদের দুটি হাত ,হাতের আঙ্গুল ৫টি ,তার মাঝে ৮টি আঙ্গুল আছে যেগুলো কিনা তিনটি ভাগে বিভক্ত।যার প্রতিটিই ফিবোনাচ্চি সংখ্যা।


ফিবোনাচ্চি নিয়ে বলে শেষ করা যাবেনা। ধারণা করা হয় প্রকৃতির অনেক কিছুই ফিবোনাচ্চি সিরিজকে অনুসরণ করে। তাছাড়া গণিতের বেশ কিছু জটিল সমস্যা সমাধানে ফিবোনাচ্চি খুবই সাহায্যকারী। ডাটা স্ট্রাকচার এও অনেক সমস্যা ফিবোনাচ্চি সিরিজ দিয়ে সমাধান করা যায়। তবে গতকালকের একটি পোস্ট এ দেখলাম পাখির ঝাঁক, ইদুর বিড়াল এর সংখ্যা ফিবোনাচ্চি এর সাথে মিলে। তা ভুল ধারনা। তবে ফিবোনাচ্চি ইদুরের উপর গবেষণা চালিয়ে দেখেছিলেন যে তারা ফিবোনাচ্চি ক্রম অনুসারে বংশবৃদ্ধি করে। ভবিষ্যতে সময় পেলে এই নিয়ে আরো লেখার চেষ্টা করব।

 

লেখাটির বিষয়বস্তু(ট্যাগ/কি-ওয়ার্ড): গণিত ;
সর্বশেষ এডিট : ২৫ শে এপ্রিল, ২০০৯ সন্ধ্যা ৬:৪৩ | বিষয়বস্তুর স্বত্বাধিকার ও সম্পূর্ণ দায় কেবলমাত্র প্রকাশকারীর...

 

 

মোট সময় লেগেছে ১.০০২৯ সেকেন্ড

Enter your search terms