অংক বিষয়টা আমার কাছে সবসময়ই খুব রহস্যময়। বিভিন্ন সময়ে, বিভিন্ন বয়সে এর বিভিন্ন রকমের রহস্যময়তা দেখেছি, আর আশ্চর্য হয়ে ভেবেছি, সৃষ্টির সব রহস্য বোধহয় অংকের মধ্যেই নিহিত। ছোটবেলায় পাটিগণিত করতে গিয়ে চোখের পানি, নাকের পানি মাঝেমধ্যেই এক হয়ে যেত। আবার সমাধান করতে পারলে অনাবিল আনন্দ পেতাম। অংক ভালোবাসতাম খুবই, আর সেই ভালোবাসাকে অনেক গুন বাড়িয়ে দিয়েছিলেন আমার আব্বা। উনি ছিলেন অংকে অত্যন্ত পারদর্শী একজন মানুষ, যার হাত ধরেই অংকে আমার হাতেখড়ি। ইন্টারমিডিয়েটে এসে স্ট্যাটিক্স আর ডায়নামিক্স এর খপ্পড়ে পড়ে অংকের প্রতি আকর্ষণ কমে যায়, তবে ভালোবাসা কমে নাই। খুবই ইচ্ছা ছিল এপ্লায়েড ফিজিক্স নিয়ে পড়ার। কিন্তু কিছুটা ভয়ের কারনেই বলা চলে, ঢাকা বিশ্ববিদ্যালয়ে ভর্তি হলাম কমার্স ফ্যাকাল্টিতে; ফাইন্যান্স ডিপার্টমেন্টে। অবশ্য ঘনিষ্ঠ বন্ধুদের সবার কমার্স ফ্যাকাল্টিতে চলে আসাও একটা বড় কারন ছিল। এখানেও অংক, তবে ভিন্ন ধরনের।

সে যাই হোক, অত্যন্ত আগ্রহ থাকা সত্বেও এখন অংক নিয়ে বিভিন্ন আর্টিকেল তেমন করে পড়তে পারি না। সবাই জানে, বিদেশের জীবন কতোটা কঠিন। সংসারের কাজে সাহায্য পাওয়ার সুবিধা একেবারেই নাই এখানে। এ টু জেড, প্রতিটা কাজ নিজেকেই করতে হয়। দিনের দৈর্ঘ্য সবজায়গাতেই ২৪ ঘন্টা, টেনে লম্বা করার কোন উপায় নাই! কাজেই বুঝতেই পারছেন, সংসার, কাজ, ব্লগিং ইত্যাদি করার পর ঘুমানোর সময়ই ঠিকমতো পাই না! বিভিন্ন লেখা মাথার মধ্যে ঘোরাফেরা করে। লেখার সময় যতোক্ষন বের করতে না পারি, মাথার মধ্যে যন্ত্রণা দেয়। ঝেড়ে ফেলতে পারলে সাময়িক উপশম পাওয়া যায়। অনেকদিনের পুষে রাখা তেমনই একটা যন্ত্রণা ঝেড়ে ফেলছি আজ। ভূমিকা পড়ে এতোক্ষণে বুঝে গিয়েছেন নিশ্চয়ই, এটা অংক বিষয়ক পোষ্ট! ইয়েস…..আমার প্রিয় একটা বিষয়বস্তু, ফিবোনাচ্চি রাশিমালা এবং এর রহস্যময়তা।

প্রথমেই ছোট্ট করে একটু ইতিহাস বলি। ফিবোনাচ্চি রাশিমালার সবচেয়ে পুরানো ধারনা পাওয়া যায় ভারতবর্ষে। আচার্য পিংগালা সর্বপ্রথম উনার 'চন্দশাস্ত্র' গ্রন্থে (৪৫০ খৃষ্টপূর্বাব্দ – ২০০ খৃষ্টপূর্বাব্দ) এ'সম্পর্কে ধারনা দেন। পরবর্তীতে ভারত মুনী 'নাট্যশাস্ত্র' গ্রন্থে (১০০ খৃষ্টপূর্বাব্দ – ৩৫০ খৃষ্টাব্দ) এবং গোপাল (১১৩৫ খৃষ্টাব্দ) কর্তৃক প্রকাশিত গণিতজ্ঞ ভিরাঙ্ক এর কাজে এ'সম্পর্কিত পরিস্কার ধারনা পাওয়া যায়।

ভারতবর্ষের বাইরে ১২০২ খৃষ্টাব্দে ইতালীর পিসা নগরীর লিওনার্দো 'লাইবার আবাসি' নামে গণিতের উপর একটা গ্রন্থ লিখে সাড়া ফেলে দেন। জেনে রাখা ভালো, পশ্চিমে ইন্দো-আরবীয় সংখ্যাতত্ব বর্ণনা এবং আরবীয় সংখ্যাগুলোর ব্যবহার নিয়ে তখন পর্যন্ত যেসব বই লেখা হয়েছিল তার মধ্যে এই বইটা ছিল অগ্রগন্য। মধ্যযুগের সবচাইতে মেধাবী গণিতজ্ঞ হিসাবে বিবেচিত লিওনার্দোর মৃত্যুর অনেক পরে ১৮৩৮ সালে ফ্রাঙ্কো-ইতালিয়ান ইতিহাসবিদ এবং গণিতজ্ঞ গিউম লিব্রি উনাকে 'ফিবোনাচ্চি' নামে অভিহিত করেন। এই বইতে উনি একটা নির্দিষ্ট সময়ে খরগোশের সংখ্যাবৃদ্ধির সিকোয়েন্স বা সংখ্যাক্রম নিয়ে আলোচনা করেন যেটা পরবর্তীতে ফিবোনাচ্চি সিকোয়েন্স বা রাশিমালা হিসাবে বিখ্যাত হয়ে ওঠে। কি এই সিকোয়েন্স বা রাশিমালা?

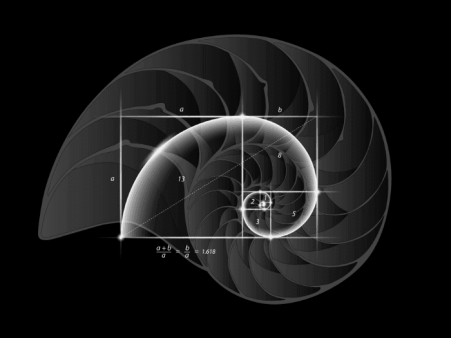
এই সিকোয়েন্স অনুযায়ী, প্রতিটা সংখ্যা হবে আগের দু'টা সংখ্যার যোগফল, আর এটা শুরু হবে ০ এবং ১ দিয়ে। কাজেই সংখ্যাক্রম হবে, (০,১): ১, ২, ৩, ৫, ৮, ১৩, ২১, ৩৪, ৫৫, ৮৯, ১৪৪………..। এই রাশিমালার আবিস্কারের ফলে গণিত এবং গণিতের আরেকটা শাখা, জ্যামিতির বহু জট খুলে গিয়েছিল এবং আশা করা যায়, ভবিষ্যতে আরও খুলবে। তবে, এই পোষ্টে সেসব জট খোলা আমার আলোচ্য বিষয় না। আমার এই পোষ্টের মূল ফোকাস হলো গোল্ডেন রেশিও। অত্যন্ত রহস্যে ভরা (অন্তত আমার কাছে) এই গোল্ডেন রেশিও একসময় আমার মাথা খারাপ করে দিয়েছিল (এখনও করে, তবে বেশী মাথা ঘামাই না)।

ধরে নেয়া যায়, আপনারা সবাই পাই (π) চিনেন, এটা একটা অনুপাত বা রেশিও। আরেকটু বলি। এটা একটা অমূলদ সংখ্যা (irrational number) যার মান হচ্ছে 3.14159265358979…...। অমূলদ বা ইররেশন্যাল অর্থ হলো এর দশমিকের পরের ডিজিটগুলো অসীম এবং কোন প্যাটার্নের পুনরাবৃত্তি করবে না। ফাই (Φ) ও তেমনই একটা জিনিস, পাই এর খালাতো ভাই বলতে পারেন, যার মান 1.618033988749895…….। এটাই গোল্ডেন রেশিও, আর এটা পাওয়া যায় ফিবোনাচ্চি সিকোয়েন্স থেকে।

কিভাবে? আসেন তাহলে একটা নতুন সিকোয়েন্স বানাই। ফিবোনাচ্চির প্রতিটা সংখ্যাকে যদি আগের সংখ্যা দিয়ে ভাগ করি, তাহলে যে সিকোয়েন্সটা পাওয়া যায় তা এমন,

১/১= ১, ২/১= ২, ৩/২= ১.৫, এবং এভাবে ১.৬৬৬…, ১.৬, ১.৬২৫…, ১.৬১৫…, ১.৬১৯…, ১.৬১৭…, ১.৬১৮১…, ১.৬১৭৯…. ইত্যাদি।

সুতরাং সূত্রটা হলো,
A/B = (A+B)/A = 1.618033987 = Φ

যদিও ফাই এর মান ফ্লেক্সিবল বা নমনীয়, কিন্তু এটা 1.618033987 এর আশেপাশেই থাকবে। তাই এটাকে মোটামুটি স্ট্যান্ডার্ড ধরে নেয়া হয়। নমনীয়তার কারনে মানে যে হেরফের হয় সেটা এতোই নগন্য যে উপেক্ষা করার মতো। এ তো গেল ফিবোনাচ্চি সিকোয়েন্স থেকে গোল্ডেন রেশিও পাওয়ার পদ্ধতি। কিন্তু এটা মাথা কিভাবে খারাপ করে? ওকে, সংক্ষেপে বলি। টাইট হয়ে বসেন।

এই গোল্ডেন অনুপাত প্রকৃতির সর্বত্র আছে। প্রকৃতির গঠনে এর মৌলিকত্ব এখন প্রমানীত। শতাব্দীর পর শতাব্দী ধরে এটা গণিতজ্ঞ, শিল্পী, ডিজাইনার, অর্কিটেক্ট, বিজ্ঞানী, প্রকৃতিবিদসহ বলতে গেলে সবাইকে বিমুগ্ধ করে রেখেছে। প্রাচীণ বিভিন্ন স্থাপনায় এটার ব্যবহার দেখা যায়। সঙ্গীতে, চিত্রকলায়ও এর ব্যবহার বহুল পরিমানে। মানুষের শরীরের এনাটমি, ফুল-ফল-বৃক্ষের গঠন, স্পাইরাল ফর্মের বিভিন্ন জীব যেমন, শামুক; সব্জি, যেমন ফুলকপি, বাধাকপি; গাছের বৃদ্ধি, মহাশুন্যের গঠন, সামুদ্রিক ঘুর্ণিঝড়, এমনকি মানুষের ডিএনএ এর গঠন কোনকিছুই এই গোল্ডেন রেশিওর বাইরে নয়। উদাহরন দিয়ে শেষ করা যাবে না। ইন্টারনেটের যুগ। আগ্রহীরা চাইলে 'গোল্ডেন রেশিও' লিখে সার্চ দেন, প্রচুর পেয়ে যাবেন….প্রচুর!

একটা ছোট্ট পরীক্ষা চাইলে আপনি এখনই করতে পারেন। মাথা থেকে পা পর্যন্ত মাপেন, এখন মাটি থেকে নাভি পর্যন্ত মেপে যা পাবেন তা দিয়ে ভাগ দেন….গোল্ডেন রেশিও পাবেন। অথবা, মাটি থেকে হিপের মাপকে মাটি থেকে হাটুর মাপ দিয়ে ভাগ দেন। তবে মনে রাখতে হবে, যেহেতু ম্যানুয়েলী মাপছেন, মাপ শতভাগ সঠিক হবে না। কাজেই কাছাকাছি কোন একটা ভ্যালু পাবেন।

প্রকৃতির সর্বত্র এটা থাকায় 'কাকতালীয় ব্যাপার' ধারনাটা বাতিল করে দেয়া যায়। তাই প্রাচীণকালের মানুষেরা মনে করতো এই অনুপাতটি সৃষ্টিকর্তা আগে থেকেই ঠিক করে দিয়েছেন। সেজন্যে তখনকার বিজ্ঞানীরা এটাকে স্বর্গীয় অনুপাতও বলতেন। এখন আমরা আধুনিক হয়েছি। এসব পুরানো ধ্যান-ধারনা মানতে যাবো কোন দুঃখে? তবে, কিছু কিছু লোক সবযুগেই ঝামেলা পাকানোর চেষ্টা করে। তারা প্রশ্ন করবে, এই ম্যাথমেটিক্যাল প্যাটার্ন বা অংকটা হোমো সেপিয়েন্সরা কোন এক পর্যায়ে আবিস্কার করে ফেললেও এটা তো প্রকৃতিতে আগেই ছিল। এই নিখুত কর্মটি করলো কে?

যারা বুঝবে, তাদের কাছে এটা বুঝপাতা; আর যারা বুঝবে না………….থাক, আর কিছু কমু না , নিজেই বুইজ্জা লন!!!


তথ্য এবং ছবিঃ অন্তর্জাল।